P8346 「Wdoi-6」最澄澈的空与海

[](https://thwiki.cc/%E5%8D%AF%E9%85%89%E4%B8%9C%E6%B5%B7%E9%81%93_%EF%BD%9E_Retrospective_53_minutes.) 广重号载着二人向东飞驰。毫无噪音，毫无摇摆，只是一个劲向东飞驰。在“万景幕”装置之下，尽管是全地下的卯酉东海道，乘客们也能饱览美丽的富士山和太平洋的景色。 但是，从这列卯酉新干线『广重』上看到的极富日本风味的美丽情景，对于梅莉来说，只不过是无趣的视觉刺激罢了。高动态范围的影像也好，极富日本风味的情景也好，都敌不过真正的天空的颜色。 身与华落，心将香飞。即便肉体会像花朵一样终有一天凋落，但心却可以如花香一般飘往远方。 「梅莉，你看，天上的星星呦。」

### 简要题意 给定 $2n$ 个点、$m$ 条边的[二分图](http://oi-wiki.com/graph/bi-graph/#_1)（可能有重边），左部点与右部点个数相同，判断其完美匹配数量是否**恰好**为 $1$。是则输出 `Renko`，否则输出 `Merry`。 > **注**：完美匹配是指，从边集中选出 $n$ 条边，这些边的顶点组成的点集恰好覆盖了所有的 $2n$ 个点。 --- ### 原始题意 在夜里，莲子与梅莉来到了东京的海边，躺在沙滩上，欣赏着澄澈的天空与大海，数起了天上的星星。 在这些星星之中，有 $n$ 个星星 $\{a_i\}$，是莲子先发现的，被称为莲子星；而又有 $n$ 个星星 $\{b_i\}$，是梅莉先发现的，被称为梅莉星。由于她们心有灵犀，这两批星星之间**不存在交集**。 她们发现，有一些莲子星，与一些梅莉星之间恰好存在运动关系。具体而言，这些关系一共有 $m$ 组，每一组关系形如 $(u_i,v_i)$，也就是说第 $u_i$ 颗莲子星与第 $v_i$ 颗梅莉星之间存在运动关系。这些运动关系有可能重复。 这让莲子和梅莉非常好奇。作为专攻超统一物理学的女大学生，莲子认为，如果认为这些星星的运动是**和谐**的，那么她应当能够从这 $m$ 个运动关系中，找出若干个运动关系，使得**每颗**星星**都被**这些运动关系**包含**的同时，不会有一颗星星**被包含在两个**运动关系之中。 然而，梅莉认为，**和谐**的运动可能是不存在的，更何况即使莲子找到了**和谐**的运动，莲子也无法确保这种和谐运动的**唯一性**。两种和谐运动不同，当且仅当选取出的两组运动关系中，存在至少一个运动关系，是不相同的。 因为意见不合，她们于是打情骂俏了一顿。莲子于是记下了她们所看到了星星和她们之间的运动关系，并且找到了已经证明了 P=NP 的你，希望你能告诉她们，最后是谁正确呢？

无

无

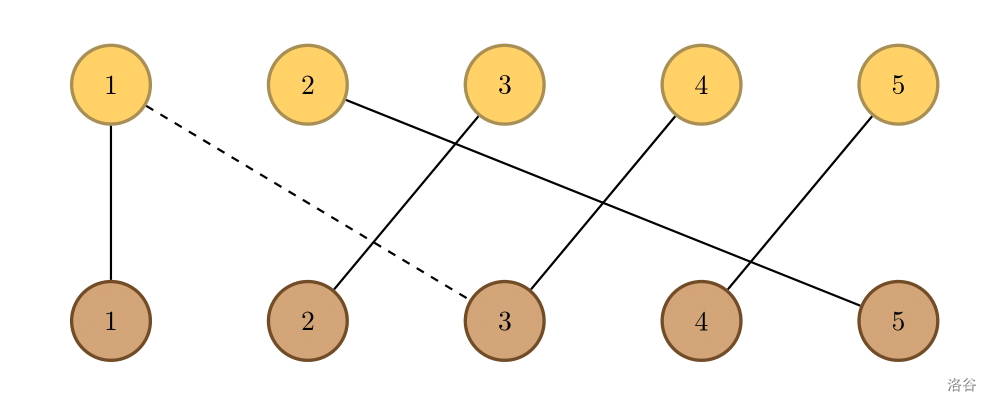
### 样例解释 #### 样例 \#1  如图所示，存在唯一的方案：$\{1\to 1,2\to 5,3\to 2,4\to 3,5\to 4\}$。 ### 数据范围 **本题采用捆绑测试。** $$ \def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|c|}\hline \textbf{Subtask} & \textbf{\textsf{分值}} & \bm{n\le } & \bm{m\le} & \textbf{\textsf{特殊性质}} & \textbf{Subtask \textsf{依赖}}\cr\hline 1 & 10 & 10 & 10 & - & - \cr\hline 2 & 20 & 300 & 4\times 10^4 & - & 1\cr\hline 3 & 20 & 10^5 & 5 \times 10^5 & \mathbf{A} & - \cr\hline 4 & 20 & 10^5 & 2 \times 10^5 & \mathbf{B} & - \cr\hline 5 & 30& 10^6 & 2\times 10^6 & - & 2,3,4 \cr\hline \end{array} $$ - 特殊性质 $\mathbf{A}$：保证对于第 $i$ 颗莲子星，与第 $i$ 颗梅莉星之间存在运动关系。 - 特殊性质 $\mathbf{B}$：保证 $m=2n-1$。 对于 $100\%$ 的数据，保证 $1 \le u_i,v_i\le n \le 10^6$，$1 \le m \le 2 \times 10^6$，$1 \leq T \leq 5$ 且对于每个测试点，$\sum m \leq 4 \times 10^6$。 对于 $\rm Subtask\ 5$，时间限制为 $3$ 秒。其它测试点时间限制为 $1$ 秒。