[蓝桥杯 2022 国 A] 环境治理

LQ 国拥有 $n$ 个城市，从 $0$ 到 $n - 1$ 编号，这 $n$ 个城市两两之间都有且仅有一条双向道路连接，这意味着任意两个城市之间都是可达的。每条道路都有一个属性 $D$，表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时，可能存在多条路线，每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘度之和，LQ 国的人都很讨厌灰尘，所以他们总会优先选择灰尘度最小的路线。 LQ 国很看重居民的出行环境，他们用一个指标 $P$ 来衡量 LQ 国的出行环境，$P$ 定义为： $$P=\sum \limits_{i=0}^{n-1} \sum \limits_{j=0}^{n-1} d(i,j)$$ 其中 $d(i,j)$ 表示城市 $i$ 到城市 $j$ 之间灰尘度最小的路线对应的灰尘度的值。 为了改善出行环境，每个城市都要有所作为，当某个城市进行道路改善时，会将与这个城市直接相连的所有道路的灰尘度都减少 $1$，但每条道路都有一个灰尘度的下限值 $L$，当灰尘度达到道路的下限值时，无论再怎么改善，道路的灰尘度也不会再减小了。 具体的计划是这样的： - 第 $1$ 天，$0$ 号城市对与其直接相连的道路环境进行改善； - 第 $2$ 天，$1$ 号城市对与其直接相连的道路环境进行改善； …… - 第 $n$ 天，$n - 1$ 号城市对与其直接相连的道路环境进行改善； - 第 $n + 1$ 天，$0$ 号城市对与其直接相连的道路环境进行改善； - 第 $n + 2$ 天，$1$ 号城市对与其直接相连的道路环境进行改善； …… LQ 国想要使得 $P$ 指标满足 $P \leq Q$。请问最少要经过多少天之后，$P$ 指标可以满足 $P \leq Q$。如果在初始时就已经满足条件，则输出 $0$；如果永远不可能满足，则输出 $-1$。

输入的第一行包含两个整数 $n, Q$，用一个空格分隔，分别表示城市个数和期望达到的 $P$ 指标。 接下来 $n$ 行，每行包含 $n$ 个整数，相邻两个整数之间用一个空格分隔，其中第 $i$ 行第 $j$ 列的值 $D_{i,j} (D_{i,j}=D_{j,i},D_{i,i} = 0)$ 表示城市 $i$ 与城市 $j$ 之间直接相连的那条道路的灰尘度。 接下来 $n$ 行，每行包含 $n$ 个整数，相邻两个整数之间用一个空格分隔，其中第 $i$ 行第 $j$ 列的值 $L_{i,j} (L_{i,j} = L_{j,i}, L_{i,i} = 0)$ 表示城市 $i$ 与城市 $j$ 之间直接相连的那条道路的灰尘度的下限值。

输出一行包含一个整数表示答案。

3 10
0 2 4
2 0 1
4 1 0
0 2 2
2 0 0
2 0 0

2

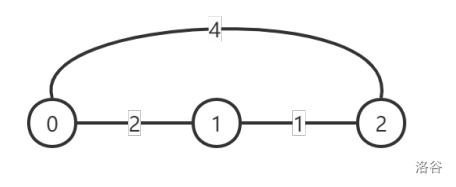
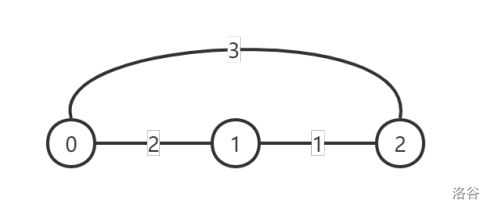
**【样例说明】** 初始时的图如下所示，每条边上的数字表示这条道路的灰尘度：  此时每对顶点之间的灰尘度最小的路线对应的灰尘度为： - $d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 3$； - $d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 1$； - $d(2, 0) = 3, d(2, 1) = 1, d(2, 2) = 0$。 初始时的 $P$ 指标为 $(2 + 3 + 1) \times 2 = 12$，不满足 $P \leq Q = 10$; 第一天，$0$ 号城市进行道路改善，改善后的图示如下：  注意到边 $(0, 2)$ 的值减小了 $1$，但 $(0, 1)$ 并没有减小，因为 $L_{0,1} = 2$ ，所以 $(0, 1)$ 的值不可以再减小了。此时每对顶点之间的灰尘度最小的路线对应的灰尘度为： - $d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 3$， - $d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 1$， - $d(2, 0) = 3, d(2, 1) = 1, d(2, 2) = 0$。 此时 $P$ 仍为 $12$。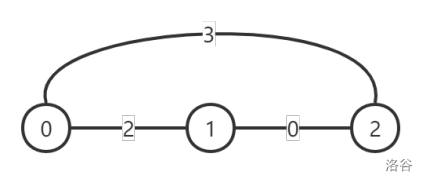 第二天，1 号城市进行道路改善，改善后的图示如下：  此时每对顶点之间的灰尘度最小的路线对应的灰尘度为： - $d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 2$， - $d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 0$， - $d(2, 0) = 2, d(2, 1) = 0, d(2, 2) = 0$。 此时的 $P$ 指标为 $(2 + 2) \times 2 = 8 < Q$，此时已经满足条件。 所以答案是 $2$。 **【评测用例规模与约定】** - 对于 $30\%$ 的评测用例，$1 \leq n \leq 10$，$0 \leq L_{i,j} \leq D_{i,j} \leq 10$； - 对于 $60\%$ 的评测用例，$1 \leq n \leq 50$，$0 \leq L_{i,j} \leq D_{i,j} \leq 10^5$； - 对于所有评测用例，$1 \leq n \leq 100$，$0 \leq L_{i,j} \leq D_{i,j} \leq 10^5$，$0 \leq Q \leq 2^{31} - 1$。 蓝桥杯 2022 国赛 A 组 F 题。