[传智杯 #4 初赛] 小卡与落叶

坐在飞驰的火车上，望着窗外泛黄的树叶，“又是一个冬天”，小卡心想。这是一个万物凋零的季节，一阵寒风刮过，树叶就被染黄了，再一阵寒风刮过，便是满地金黄。 百无聊赖之际，小卡发现，树叶变黄是有规律的，每一颗树，只有下面一半是黄的，上半部分都是绿的。小卡心想，该怎么统计黄色的叶子个数呢？

给你一棵有 $n(1\le n\le 10^5)$ 个结点的有根树，根结点标号为 $1$，根节点的深度为 $1$，最开始整棵树的所有结点都是绿色的。 小卡有 $m(1\le m \le 10^5)$ 个操作。 操作一：把整棵树都染绿，之后让深度 $\ge x$ 的结点变黄。 操作二：询问一个结点 $x$ 的子树中有多少个黄色结点。

第一行两个正整数 $n,m$，表示树的结点个数和操作个数。 接下来 $n-1$ 行，每行两个正整数 $x,y$，表示树上的一条边。 接下来 $m$ 行，每行两个正整数 $op,x(1\le x\le n)$，如果 $op=1$ 则表示操作一，否则表示操作二。

对于每个操作二，输出一行一个正整数，表示 $x$ 的子树中黄色结点的个数。

5 9
1 2
1 3
2 4
4 5
1 3
2 5
2 2
2 1
1 2
2 1
2 4
2 5
2 2

1
2
2
4
2
1
3

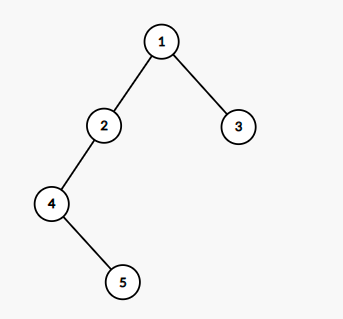
样例一中的树如下：  第一次染色将 $4$ 和 $5$ 染为黄色，查询 $5,2,1$ 三个点的子树，答案分别为 $1,2,2$。 第二次染色将 $2,3,4,5$ 染为黄色，查询 $1,4,5,2$ 四个点的子树，答案分别为 $4,2,1,3$。