[传智杯 #5 初赛] G-二人的花纹纸游戏

梅莉买到了一张特殊的带有花纹的纸。整张纸的图案可以视为，由一个较小的图案，沿着横向与纵向无限循环而成。同时，这个基本图案部分透明，部分不透明。 于是，如果将这张纸覆盖在书本上，那么一些字可以被看见，另一些字看不见。 莲子突发奇想：假使她制作一张很大很大的数表，将花纹纸覆盖在上面，那么就会有很多数字被遮挡。那些没有被遮挡的数字的和是多少呢？

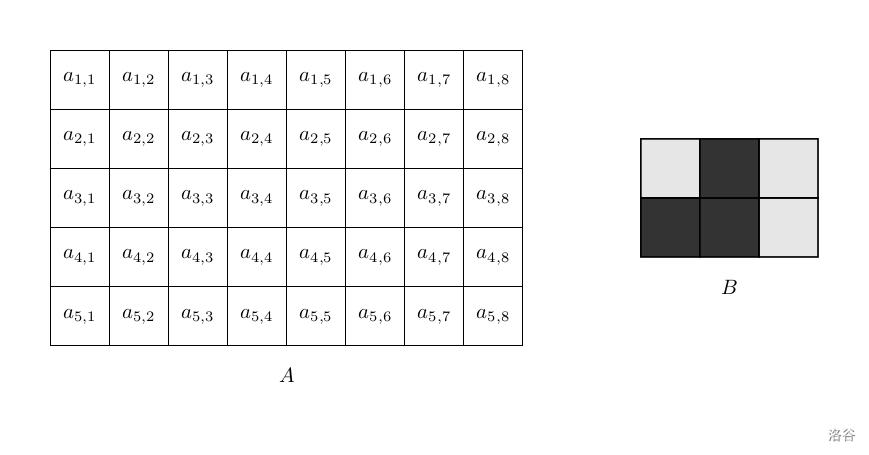
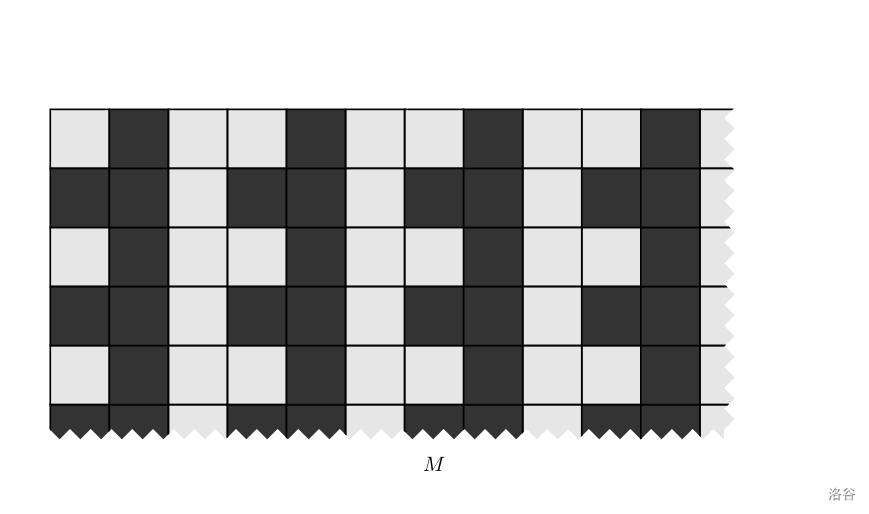
事实上，二人的问题可以转化成如下描述：给定一个 $n$ 行 $m$ 列的普通矩阵 $A$，以及一个 $r$ 行 $c$ 列的 $01$ 矩阵 $B$。$B$ 中为 $1$ 的格子是黑色，不透明；为 $0$ 的格子是透明的。  使用 $B$ 矩阵，循环生成一个**无穷大**的矩阵 $M$：  现在有 $q$ 次询问。每次将 $M$ 矩阵左上角和 $(x_1,y_1)$ 对齐，此时此时会有一些 $A$ 中的元素被遮挡，另一些元素可以被看见。  求出此时，$A$ 当中以 $(x_1,y_1)$ 作为左上角，$(x_2,y_2)$ 作为右下角的子矩阵中，可以被看见的元素之和。结果对 $998{,}244{,}353$ 取模。 在上面的例子里，$(x_1,y_1)=(2,3)$，$(x_2,y_2)=(4,7)$。可以被看见的元素之和为 $a_{2,3}+a_{2,5}+a_{2,6}+a_{3,5}+a_{4,3}+a_{4,5}+a_{4,6}$。 ### 形式化题面 给定一个 $n$ 行 $m$ 列的普通矩阵 $A$，以及一个 $r$ 行 $c$ 列的 $01$ 矩阵 $B$。使用 $B$ 矩阵，生成一个**无穷大**的矩阵 $M$： $$M= \begin{pmatrix} B & B & B &\cdots \\ B & B & B &\cdots \\ B & B & B &\cdots \\ \vdots &\vdots &\vdots & \end{pmatrix} =\begin{pmatrix} b_{1,1} & b_{1,2} & \cdots & b_{1,c} & b_{1,1} & b_{1,2} & \cdots & b_{1,c} & b_{1,1} & \cdots \\ b_{2,1} & b_{2,2} & \cdots & b_{2,c} & b_{2,1} & b_{2,2} & \cdots & b_{2,c} & b_{2,1} & \cdots \\ \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots & \\ b_{r,1} & b_{r,2} & \cdots & b_{r,c} & b_{r,1} & b_{r,2} & \cdots & b_{r,c} & b_{r,1} & \cdots \\ b_{1,1} & b_{1,2} & \cdots & b_{1,c} & b_{1,1} & b_{1,2} & \cdots & b_{1,c} & b_{1,1} & \cdots \\ b_{2,1} & b_{2,2} & \cdots & b_{2,c} & b_{2,1} & b_{2,2} & \cdots & b_{2,c} & b_{2,1} & \cdots \\ \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots & \\ b_{r,1} & b_{r,2} & \cdots & b_{r,c} & b_{r,1} & b_{r,2} & \cdots & b_{r,c} & b_{r,1} & \cdots \\ \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots & \\ \end{pmatrix}$$ 现在有 $q$ 次询问，每次给出一个子矩阵的左上角坐标 $(x_1,y_1)$ 和右下角坐标 $(x_2,y_2)$，你需要求出： $$S=\left(\sum_{i=x_1}^{x_2}\sum_{j=y_1}^{y_2}a_{i,j}\times [M_{i-x_1+1,j-y_1+1}=0] \right)\bmod 998{,}244{,}353$$ 其中 $[P]$ 表示艾弗森括号。若 $P$ 为真，则 $[P]=1$，否则 $[P]=0$。

- 第一行有两个正整数 $n,m$，描述矩阵 $A$ 的大小。 - 接下来 $n$ 行 $m$ 列，每行一个非负整数，描述 $A$ 中的元素 $a_{i,j}$。 - 下一行有两个正整数 $r,c$，描述矩阵 $B$ 的大小。 - 接下来 $r$ 行 $c$ 列，每行一个非负整数，描述 $B$ 中的元素 $b_{i,j}$。 - 下一行有一个正整数 $q$，表示询问的次数。 - 接下来 $q$ 行，每行有四个正整数 $x_1,y_1,x_2,y_2$，描述一组询问。保证 $x_1\le x_2$，$y_1\le y_2$。

- 输出共 $q$ 行。每行输出该次询问的答案。

3 4
1 2 3 4
5 6 7 8
9 10 11 12
2 2
1 0
0 1
2
1 1 3 4
1 2 3 3

40
20

4 4
1 3 2 4
5 4 2 3
4 1 2 3
3 4 4 3
1 3
1 0 0
3
1 1 3 4
2 2 4 4
1 2 3 2

14
17
0

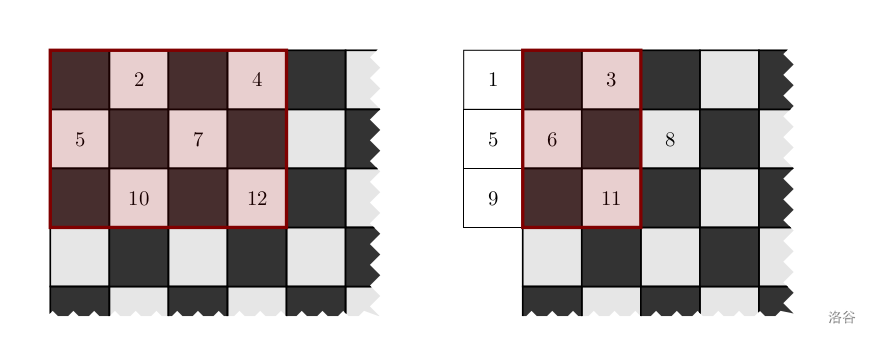
### 样例 1 解释  - 对于第一次询问，结果为 $2+4+5+7+10+12=40$； - 对于第二次询问，结果为 $3+6+11=20$。 ### 数据范围及约定 对于全部数据，保证 $1\le n,m\le 10^3$，$1\le q\le 10^4$，$1\le r,c\le 50$，$0\le a_{i,j}<998{,}244{,}353$，$b_{i,j}\in\{0,1\}$。