[传智杯 #5 初赛] I-不散的宴会
题目背景
学校正在组织宴会。
莲子和梅莉发现,学校的结构十分复杂。学生之间存在着部门与上司的关系。每一个部门内部,都呈现出连成一条线的上司关系。一个部门内等级最高的学生,又可能受限于另外某个部门内的某个学生。
莲子和梅莉同样参加了宴会。但是她们对参加学生有自己的评判。例如,她对某些部门比较喜欢,对另一些部门则不感兴趣。同时对位居不同等级的学生同样有着不同的看法。
正如某个经典问题所描述的一样,每个学生都不希望与自己的直接上司共同参加宴会。
梅莉想要知道,最好情况下,有多少个参加宴会的学生是她喜欢的。
题目描述
学生社会可以被看作一个排列成等腰直角三角形的节点阵列。该节点阵列共有 $n$ 行,第 $i$ 行共有 $i$ 个节点。我们将第 $i$ 行第 $j$ 列的节点,标号为 $(i,j)$。
- 这些节点具有权值。具体而言,节点 $(i,j)$ 的权值为 $r_i\oplus c_j$,其中 $r$ 和 $c$ 是给定的 $01$ 序列,$\oplus$ 是**二进制异或**操作。
- 这些节点有边相连。具体而言,对于 $1\le i< n$,$1\le j\le i$,会有一条边连接 $(i,j)$ 和 $(i+1,j)$。此外,对于 $2\le i\le n$,还会有边连接 $(i,i)$ 和 $(i-1,a_i)$。其中 $a$ 是给定的序列。
现在你需要从这些节点中,选出一些节点,使得这些节点间**两两不存在边相连**,最大化选出来的节点的**权值之和**。
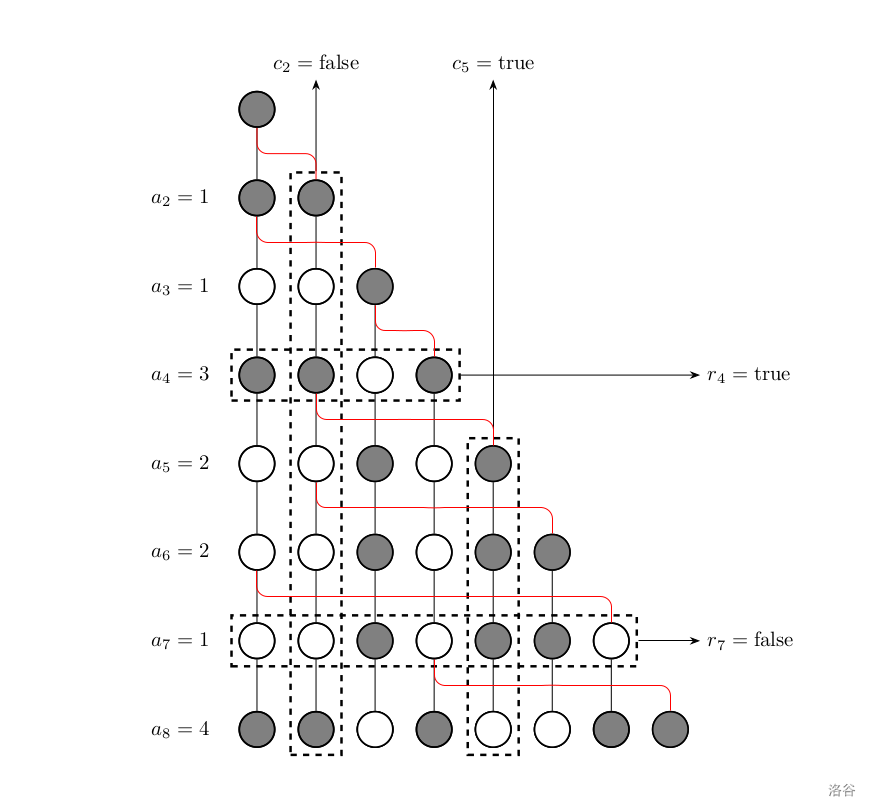
如下图所示,是 $n=8$ 的一个例子。黑色节点权值为 $1$,白色节点权值为 $0$。
**注**:图片中只象征性地给出了部分 $r_i$ 和 $c_i$ 的值。该图片上实际 $\def\t{,\allowbreak}r=\{1\t 1\t 0\t 1\t 0\t 0\t 0\t 1\}\t c=\{0\t 0\t 1\t 0\t 1\t 1\t 0\t 0\}$。
输入输出格式
输入格式
- 第一行有一个正整数 $n$,描述节点阵列的大小。
- 第二行有 $n$ 个整数 $0$ 或者 $1$,描述 $r_i$ 的值。
- 第三行有 $n$ 个整数 $0$ 或者 $1$,描述 $c_i$ 的值。
- 第四行有 $n-1$ 个正整数,其中第 $i$ 个数描述 $a_{i+1}$ 的值。
输出格式
- 输出共一行一个整数,描述选出的节点的权值之和的最大值。
输入输出样例
输入样例 #1
8
1 1 0 1 0 0 0 1
0 0 1 0 1 1 0 0
1 1 3 2 2 1 4输出样例 #1
14
说明
### 样例解释
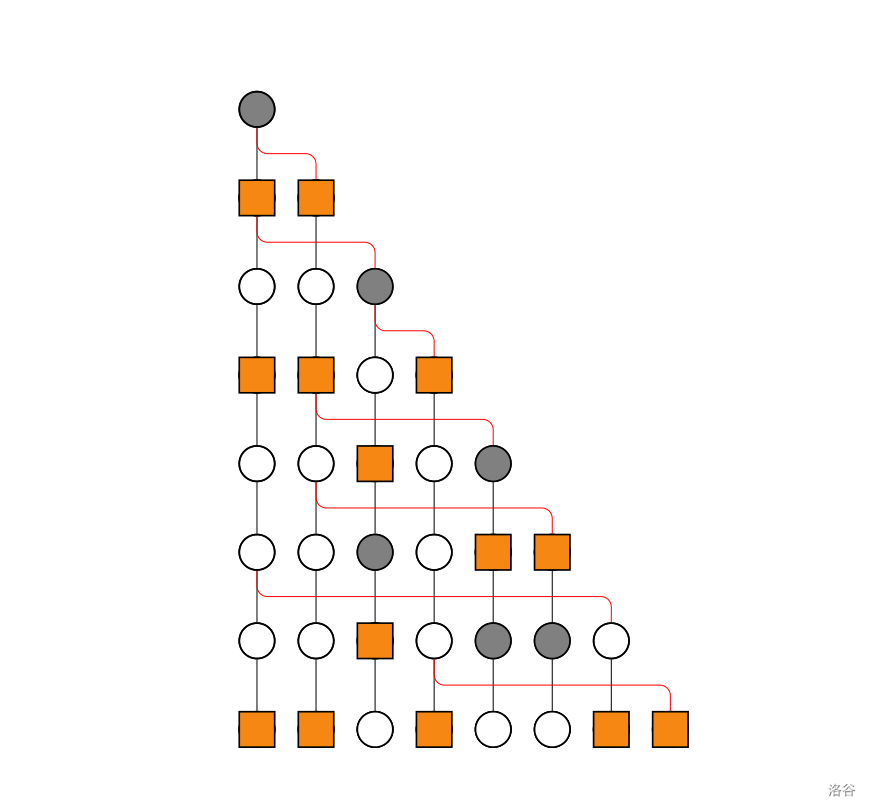
一种可能的选择方案如下图所示。橘红色方块表示选中的节点。
### 数据范围及约定
对于全部数据,保证 $1\le n\le 10^6$,$r_i\in\{0,1\}$,$c_i\in\{0,1\}$,$1\le a_i<i$。