[JRKSJ R7] TSM eerT

对于一个 $n$ 个结点的带边权的树 $T$，定义 $dis(x,y)$ 为 $T$ 中 $x\to y$ 路径上的边权和。再定义一个 $n$ 个结点的无向完全图 $p(T)=G$，其中 $\forall x,y\in [1,n]$，$G$ 中边 $(x,y)$ 的边权为 $dis(x,y)$。 定义 $f(T)$ 为 $p(T)$ 的最大生成树。特别的，若 $p(T)$ 的最大生成树不唯一，请立刻判断出并报告。 给定树 $T_0$ 和整数 $k$，求 $f^k(T_0)$。其定义将在下文给出。

第一行两个整数 $n,k$。\ 下面第 $2\sim n$ 行，第 $i$ 行两个整数 $i-f_i,v_i$ 表示 $T_0$ 的一条边 $(i,f_i)$，边权为 $v_i$。**也就是说，这一行输入了两个整数 $f'_i,v_i$，真实的 $f_i=i-f'_i$。**

输出仅有一个整数表示答案。 若 $\exists x\in[0,k-1]$ 使得 $p(f^x(T_0))$ 的最大生成树不唯一，输出 $-1$。否则，输出 $f^k(T_0)$ 的所有边权和对 $2^{32}$ 取模的结果。

3 3
1 1
2 2

13

10 2
1 7
1 2
1 5
4 5
2 1
3 9
2 9
4 4
9 4

736

4 1
1 1
2 1
3 1

-1

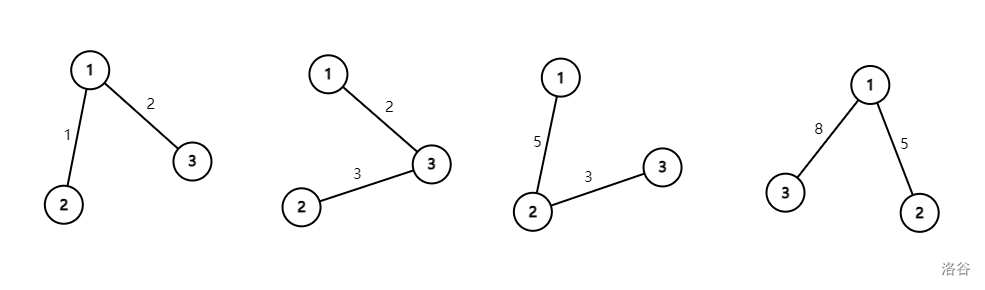
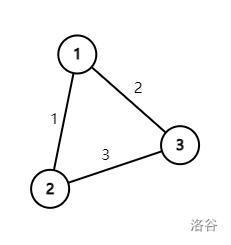
### 定义 $f^k(T)$ 的定义为： $$f^k(T)=\begin{cases}T&k=0\\f(f^{k-1}(T))&k>0\end{cases}$$ ### 样例 $1$ 解释  分别是 $T_0,f(T_0),f^2(T_0),f^3(T_0)$。 以计算 $f(T_0)$ 的过程为例，生成的 $p(T_0)=G$ 为  最大生成树上的边为 $(1,3),(2,3)$。 ### 数据规模 本题采用捆绑测试。 | $\text{Subtask}$ | $n\le$ | $k\le$ | $\text{Score}$ | | :----------: | :----------: | :----------: | :----------: | | $1$ | $10^3$ | $1$ | $10$ | | $2$ | $10^5$ | $1$ |$20$ | | $3$ | $10^6$ | $1$ |$30$ | | $4$ | $10^6$ | $10^7$ |$40$ | 对于 $100\%$ 的数据，$2\le n\le 10^6$，$1\le k\le 10^7$，$1\le f_i<i$，$1\le v_i\le10^9$。 ### 特殊评分方式 本题开启子任务依赖，具体如下： - 对于子任务 $i$，您需要答对所有 $j\in[1,i]$ 的子任务 $j$ 才能获得子任务 $i$ 的分数。