『GROI-R1』 一切都已过去

悦关上窗，拉上帘布。 果然还是想不起来啊。 隐约记得曾和什么人一起做过这样的事。 仰面躺下，手执一只木笺。 「究竟如何，才能拥有“过去”啊……」 她闭上双眼。 「6 岁前的记忆……究竟如何才能寻回？」

悦正在寻找她的记忆。忽然，她来到了有 $n$ 个节点的一棵树上。树上每一条边都有各自边权，每一个点都有各自的点权。 「把经历都聚拢起来，能完整地复原吗……」 悦从树上的一个点，慢慢地走到了另一个点，可是她什么也没找到。但是，她不知道，玘一直在远处望着她走过的道路。 玘发现，悦全程****没有走回头路****。他想把悦****走过的每一条边的边权乘起来****，可惜他发现他遇到了一个这一生未曾见到过的数字。 「为什么会这样呢？」 玘想到悦是突然出现在树上的，最初的点一定有蹊跷！他****把最初那个点的点权乘上****…… 突然，一束彼岸花的红光亮起！世界重新安静了下来。 悦看到了玘留下的字样，可惜她不能从中看出任何过去的记忆。现在，你要帮她判断：把经历都聚拢起来，****能完整地复原过去吗****？我们称悦的一条路径能“复原过去”，当且仅当玘****留下的乘积是一个整数****。 **形式化题面** 给定一棵 $n$ 个节点的树和 $q$ 次询问。每次询问给出两个整数 $x,y$，表示询问树上以 $x$ 和 $y$ 为端点的简单路径上边权乘积与点 $x$ 的点权相乘是否为整数。

第一行两个正整数 $n$ 和 $q$，表示树上有 $n$ 个节点编号为 $1\sim n$，悦在树上走了 $q$ 条路径。 接下来一行 $n$ 个非负整数表示每个点的点权 $a_i$。 接下来 $n-1$ 行每行两个正整数 $u,v$ 和一个非负实数 $w$ 表示 $u,v$ 间有一条边权为 $w$ 的边。 接下来 $q$ 行，每行两个正整数 $x,y$，表示悦从点 $x$ 开始走到了点 $y$。

对于悦的每一次询问，你需要输出一行一个字符串。如果悦能够成功复原她的过去，请输出 `Yes`，否则请输出 `No`。

5 3
1 2 3 4 5
1 2 0.1
2 3 0.20
3 4 0.5
2 5 0.99
1 5
1 4
4 3

No
No
Yes

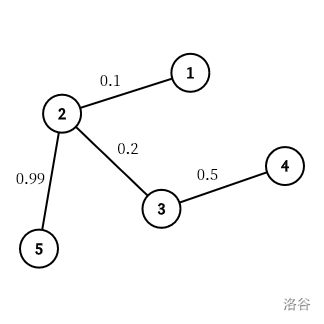
**样例解释** 根据输入可以得到下图：  对于第一个询问 $(1,5)$ 可以发现悦经过的边的边权分别是 $0.1$ 和 $0.99$，她出发的 $1$ 号点的点权为 $1$。$1\times0.1\times0.99=0.099$ 不是整数。所以输出 `No`。 对于后面两次询问同理。 **数据范围** **本题采用捆绑测试。** | 子任务编号 | 数据范围 | 特殊性质 | 分值 | | :----------: | :----------: | :----------: | :----------: | | $\text{Subtask1}$ | $n,q\le3\times 10^3$ | | $15$ | | $\text{Subtask2}$ | $n\le500$，$q\le10^5$ | | $10$ | | $\text{Subtask3}$ | $n,q\le10^5$ | $\text{BE}$ | $10$ | | $\text{Subtask4}$ | $n,q\le10^5$ | $\text{A}$ | $5$ | | $\text{Subtask5}$ | $n,q\le10^5$ | $\text{B}$ | $10$ | | $\text{Subtask6}$ | $n,q\le10^5$ | $\text{C}$ | $5$ | | $\text{Subtask7}$ | $n,q\le10^5$ | $\text{D}$ | $10$ | | $\text{Subtask8}$ | $n,q\le2×10^5$ | | $35$ | 特殊性质 $\text{A}$：保证树退化成一条链。 特殊性质 $\text{B}$：保证树随机生成（即对于每一个节点随机选择它的父亲节点）。 特殊性质 $\text{C}$：保证 $w\in\{0.1,0.3,0.5,0.7,0.9\}$。 特殊性质 $\text{D}$：保证 $w\in\{0.1,0.2,0.3,0.4,0.6,0.7,0.8,0.9\}$。 特殊性质 $\text{E}$：保证 $w\le2$ 且 $w$ 小数位数不超过 $1$ 位。 对于 $100\%$ 的数据满足 $1\le n,q\le2\times10^5$，$0\le a_i\le10^9$，$0\le w\le10^4$，$1\le u,v,x,y\le n$，$x\ne y$，$w$ 小数位数不超过 $4$ 位。