『GROI-R1』 继续深潜，为了同一个梦想

玘正在折叠床脚几件刚洗净的白衬衫，他注意到身后的声响，向右后转头看去。 以为是“外面的家伙”的他并没有刻意去遮掩自己的右眼——毕竟学院里的人不可能进来。 他看见了那个紫眸的少年；当然寒也看见了那一瞬间的鲜红。 「你什么都没看见。」 玘装作欣赏窗外的晚霞。

「世上没有无价的情报，」玘露出一丝满意的微笑。 「你懂我的意思吧？」 寒收回手。 玘给出了他留给寒的题。 > 既然紫堇和彼岸花给予了我们异色的瞳孔，我们理所应当是连接在一起的。我称**一棵树上的一个点集是“连接的”**，当且仅当**树上存在一条链能够覆盖这个点集并且这个集合大小不小于 $2$**。我们是独一无二的，可是你知道，一棵树，总是连起来的啊。 「然后呢？」 「现在，你需要告诉我每个点被多少个这样的点集所包含。」 玘飘然而去。 湖底之城那封存已久的记忆，被彼岸花和紫堇的力量，揭开了封印的一角。

第一行一个正整数 $n$ 表示这棵树有 $n$ 个点编号为 $1\sim n$。 接下来 $n-1$ 行，每行两个正整数 $u,v$ 描述一条边。

为了防止输出量过大，本题采用以下的输出方式。 设 $ans_i$ 为包含 $i$ 号节点的连接的集合的个数对 $10^9+7$ 取模得到的值，你需要输出 $\operatorname{xor}_{i=1}^n ans_i\times i$ 的值。注意这里没有取模运算。

4
1 2
2 3
2 4

18

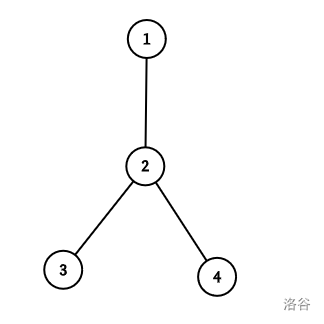
**样例解释**  **连接**的集合有以下一些： - $\{1,2\}$ - $\{1,3\}$ - $\{1,4\}$ - $\{2,3\}$ - $\{2,4\}$ - $\{3,4\}$ - $\{1,2,3\}$ - $\{1,2,4\}$ - $\{2,3,4\}$ 如 $\{1,3,4\}$ 就不是一个连接的集合，因为你找不出一条链使得 $\{1,3,4\}$ 为它的子集。 其中 $1,2,3,4$ 号节点分别在 $5,6,5,5$ 个集合中出现。通过计算可得 $\operatorname{xor}_{i=1}^n ans_i\times i=18$。 **数据范围** **本题采用捆绑测试。** | 子任务编号 | 数据范围 | 特殊性质 | 分值 | 时间限制 | | :----------: | :----------: | :----------: | :----------: | :-: | | $\text{Subtask1}$ | $n\le20$ | | $15$ | $\text{1s}$ | | $\text{Subtask2}$ | $n\le100$ | | $15$ | $\text{1s}$ | | $\text{Subtask3}$ | $n\le3\times 10^3$ | | $20$ | $\text{1s}$ | | $\text{Subtask4}$ | $n\le5\times10^5$ | $\text{A}$ | $15$ | $\text{2s}$ | | $\text{Subtask5}$ | $n\le5\times10^5$ | | $35$ | $\text{2s}$ | 特殊性质 $\text{A}$：保证树退化成一条链。 对于 $100\%$ 的数据 $1\le u,v\le n\le5\times10^5$。