『GROI-R1』 古朴而优雅

会馆内忽地安静了下来。 「敝姓言，名杉。」 他的声音沉稳而凝重，略带沙哑，却不失力度，极具穿透力。每个字都重重地打在耳畔，渗进头脑里，让人想不认真听都难。 「这所学院的院长。」

杉虽然年事已高，但是还是保持与时俱进。他学习了深度优先遍历算法，觉得这种新潮的东西在一所古朴而优雅的学院里会很受欢迎。所以，他找到了在走廊里晃荡的寒，向他提出了一个问题： 「我们知道，对一棵树进行深度优先遍历可以用下面的伪代码很好地解决。」 $$ \begin{array}{l} \text{DFS-TREE}(u)\\ \begin{array}{ll} 1 & p\gets p+1\\ 2 & t_p\gets u\\ 3 & vis_u\gets 1\\ 4 & \textbf{for }\text{each edge }(u,v)\in E \\ 5 & \qquad \textbf{if }vis_v=0\\ 6 & \qquad \qquad \text{DFS-TREE}(v)\\ 7 & p\gets p+1\\ 8 & t_p\gets u\\ \end{array} \end{array} $$ 起初，所有变量或数组的值均为 $0$。 「我们把调用 $\text{DFS-TREE}(1)$ 在遍历过程中得到的数组 $t$ 称为这棵树的**遍历顺序**。」 「你看这段代码的第 $4$ 行，这句话**遍历每一条边的顺序是不固定的**。」 寒素来最讨厌不确定的东西，可是碍于院长的颜面，还是继续听下去。 「你能数出这段代码**会生成多少种不同的遍历顺序**吗？」 寒发现他曾经做过这个题，很快地报出了解法。本以为就结束了，可是杉继续说： 「如果我**在树上增加一条边**，你还会做吗？」 寒发现他的那点水平完全不够了，于是他去请教玘。玘却认为这道题目依然很简单，他告诉了寒这道题的做法。可是寒找不到杉了。 这个世界到底怎么了呢？

第一行，两个整数 $n$ 和 $q$，表示树上有 $n$ 个结点，编号为 $1\sim n$，有 $q$ 次询问。 接下来 $n-1$ 行，每行两个整数 $u,v$，描述这棵树上的一条边。 接下来 $q$ 行，每行两个整数 $x,y$，表示在树上添加连接 $x$ 和 $y$ 的一条边，询问有多少种可能的遍历顺序。注意：每次询问是**互相独立的**，也就是说，上一次询问添加的边不会保留到下一次询问。

共 $q$ 行，每行一个整数表示这次询问的答案对 $10^9+7$ 取模后得到的值。

4 2
1 2
1 3
1 4
2 3
1 4

4
6

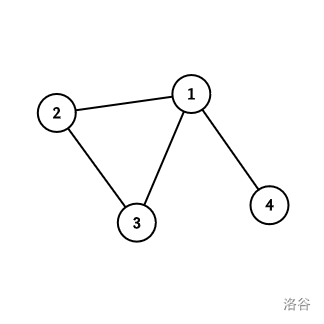
**样例解释** 对于第一次询问可以得到如图：  能得到的遍历顺序有： - $\{1,2,3,3,2,4,4,1\}$ - $\{1,4,4,2,3,3,2,1\}$ - $\{1,3,2,2,3,4,4,1\}$ - $\{1,4,4,3,2,2,3,1\}$ 对于第二次询问可以得到如图：  能得到的遍历顺序有： - $\{1,2,2,3,3,4,4,1\}$ - $\{1,2,2,4,4,3,3,1\}$ - $\{1,3,3,2,2,4,4,1\}$ - $\{1,3,3,4,4,2,2,1\}$ - $\{1,4,4,2,2,3,3,1\}$ - $\{1,4,4,3,3,2,2,1\}$ **数据范围** **本题采用捆绑测试。** | 测试点编号 | 数据范围 | 特殊性质 | 分值 | | :-----------: | :-----------: | :-----------: | :-----------: | | $\text{Subtask1}$ | $n,q\le8$ | | $5$ | | $\text{Subtask2}$ | $n,q\le20$ | | $10$ | | $\text{Subtask3}$ | $n,q\le500$ | | $10$ | | $\text{Subtask4}$ | $n,q\le3000$ | | $15$ | | $\text{Subtask5}$ | $n,q\le2\times10^5$ | $\text{A}$ | $15$ | | $\text{Subtask6}$ | $n,q\le2\times10^5$ | $\text{B}$ | $10$ | | $\text{Subtask7}$ | $n,q\le2\times10^5$ | | $35$ | 特殊性质 $\text{A}$：保证每一次询问的边 $(x,y)\in E$。 特殊性质 $\text{B}$：保证树退化成一条链。 对于 $100\%$ 的数据保证 $1\le n,q\le2\times10^5$，$1\le u,v,x,y\le n$，$x\ne y$。