P9036 「KDOI-04」挑战 NPC Ⅲ
题目背景
题目描述
小 S 有一个伟大的梦想:证明 $\text{P}=\text{NP}$。
有一天,他得知一般图最大独立集是 NPC 问题后,决定解决他。
当然小 S 太菜了,解决不了,于是求助于你:
> 给出一个含有 $n$ 个顶点,$m$ 条边的无向图 $G$,求 $G$ 中大小恰好为 $n-k$ 的独立集的数量。由于答案可能很大,请将其对 $998~244~353$ 取模。
小 S 不喜欢多测,因为他在 NOIp 中因为多测挂分,所以本题包含多组测试数据。
输入格式
无
输出格式
无
说明/提示
**【样例解释】**
对于第 $1,2$ 组测试数据,图是完全图,容易发现,完全图的最大独立集为 $1$,并且每一个顶点都单独构成一个独立集。因此第 $1$ 组测试数据的答案为 $0$,第 $2$ 组测试数据的答案为 $4$。
对于第 $3$ 组测试数据,该组数据中给出的无向图如下:
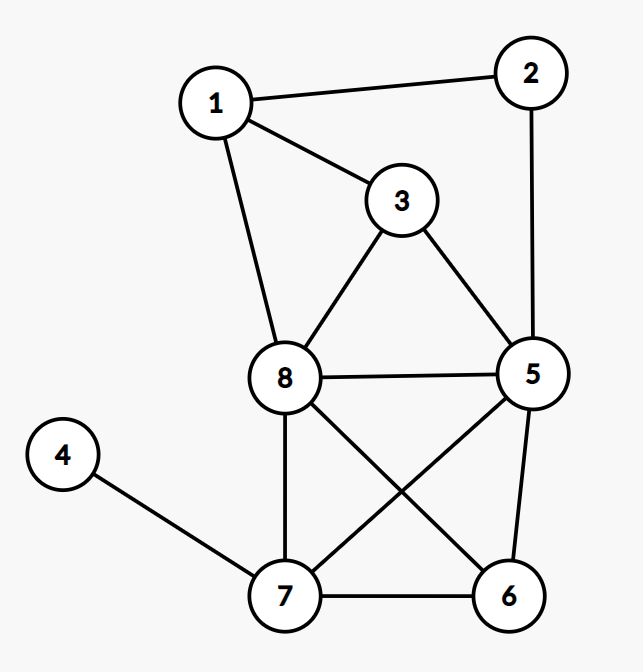
其中,所有大小为 $3$ 的独立集为:
+ $\{2,4,8\}$;
+ $\{2,3,7\}$;
+ $\{3,4,6\}$;
+ $\{2,4,6\}$;
+ $\{1,4,6\}$;
+ $\{2,3,6\}$;
+ $\{1,4,5\}$;
+ $\{2,3,4\}$。
**【数据范围】**
**本题采用捆绑测试。**
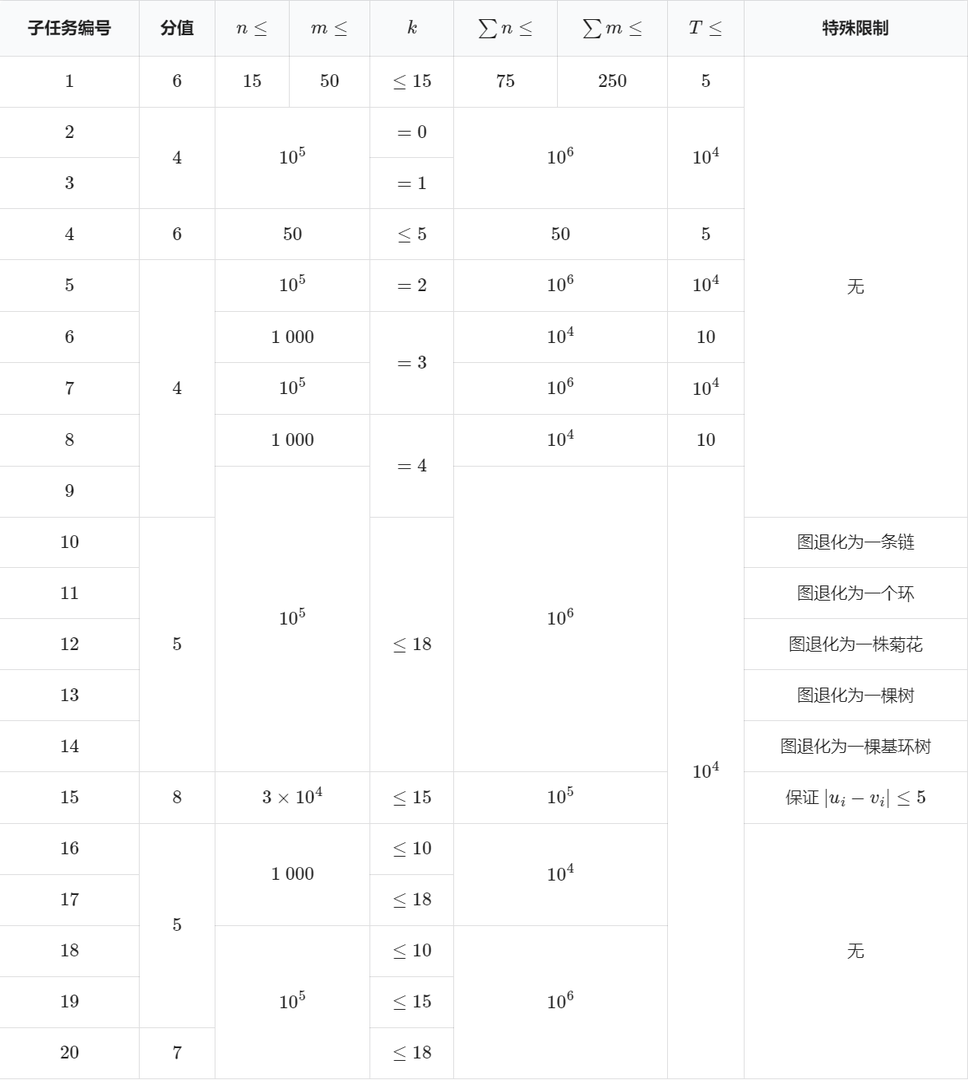
对于 $100\%$ 的数据,保证 $1\leq n\leq10^5$,$0\le m\le 10^5$,$0\leq k\leq \min(n-1,18)$,$1\leq T\leq 10^{4}$,$\sum n,\sum m\leq10^6$。
并且对于每个测试点保证:
设 $K=\max k$,即该测试点中所有 $k$ 的最大值,
+ 若 $K\ge 17$,则 $T=1$;
+ 若 $K\ge 15$,则 $T\le 3$;
+ 若 $K\ge 10$,则 $T\le 5$;
+ 若 $K\ge 5$,则 $T\le 300$。