「SvR-2」G64

定义对于两棵有根二叉树 $T_1,T_2$，$\operatorname{merge}(T_1,T_2)$ 的结果是一棵二叉树，满足其根节点的左子树为 $T_1$，右子树为 $T_2$，显然 $\operatorname{merge}(T_1,T_2)$ 的结果唯一且必然存在。 定义对于一棵有根二叉树 $T$，有函数 $G_x(T)$。其中 $G_1(T)$ 表示沿着 $T$ 的根向右儿子走，直到走到某个不存在右儿子的节点，将其右子树变为 $T$，这棵新树即为 $G_1(T)$ ，而当 $x>1$ 时，$G_x(T)$ 满足如下关系： $$G_x(T)=G_1(\operatorname{merge}(G_{x-1}(T),G_{x-1}(T)))$$ 给一棵 $n$ 个节点的以 $1$ 为根的有根二叉树，记以 $i$ 为根的子树为 $T_i$，$q$ 次询问，每次询问给定 $x,i$，求 $G_x(T_i)$ 的最大独立集。

第一行两个整数 $n,q$。 之后 $n$ 行，每行两个整数 $ls_i,rs_i$ 表示其左儿子和右儿子，若为 $0$ 则说明没有对应儿子。 之后 $q$ 行，每行两个整数 $x,i$ ，表示一次询问。

$q$ 行，每行一个数，表示这次询问的 $G_x(T_i)$ 的最大独立集大小对 $998244353$ 取模的结果。

5 3
2 3
0 4
5 0
0 0 
0 0
2 5 
2 1
1 1

5
24
6

5 1
2 3
0 4
5 0
0 0 
0 0
64 1

592424678

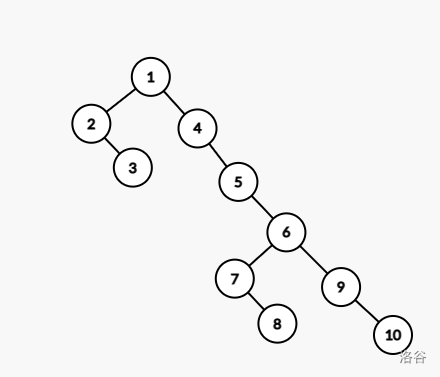
### 样例解释 对于第一组样例，$G_2(T_5)$ 的结果如下图（忽略编号）：  对于第二组样例，我有一个绝妙的解释，可惜 $G_{64}$ 太大了，这里写不下。 #### 数据规模与约定 **本题开启捆绑测试和 O2 优化。** | Subtask | 数据范围/特殊性质 | 分值 | | :------: | :------: | :------: | | $1$ | $n,q,x\le 10$| $10 \operatorname{pts}$ | | $2$ | $x =1$ | $5 \operatorname{pts}$ | | $3$ |$x\le 3$ | $10 \operatorname{pts}$ | | $4$ | $x\le 10$ | $15 \operatorname{pts}$ | | $5$ | 保证 $T_i$ 大小为 $1$ | $10 \operatorname{pts}$ | | $6$ | 无特殊限制 | $50 \operatorname{pts}$ | 对于 $100\%$ 的数据， $1\le x\le 10^9$，$1\le n\le 5\times 10^5$，$1\le q\le 5\times 10^5$。