[入门赛 #11] 移植柳树 (Hard Version)
题目背景
**本题与 Easy Version 题意完全相同,不同的地方仅在于数据范围和单个测试点内含有的测试组数量。**
HG 在上学的路上无聊的走着,看着这马路边的一排柳树,他的脑子里突然冒出了个奇怪的问题……
题目描述
假设总共有 $n$ 棵柳树,每一棵间隔都为 $x$。
现在他需要对这些树做一些操作,使得在「这 $n$ 棵树的起点不变」的同时,任意两棵树的间隔都为 $y$($y > x$)。
他被允许做的操作如下;
- 移植树木:将一个位置的树木移到另一个位置上。
如果对「起点不变」这个概念有疑惑,可以参照「样例解释」中的图例。
显然操作是需要体力的,HG 想要让尽可能多的树维持原状。现在 HG 想知道,为了达成「任意两棵树的间隔都为 $y$」这个目标,他最多可以让多少棵树保持在原来的位置。
请你帮帮他吧!
输入输出格式
输入格式
**本题单个测试点内含有多组测试数据。**
输入共 $T + 1$ 行。
第一行为一个整数 $T$,代表测试数据组数。
接下来 $T$ 行,每行三个整数 $n, x, y$,依次表示柳树的数量,未调整前每棵的间隔,想要达成的每棵的间隔。
输出格式
输出共 $T$ 行,每行一个整数,表示对于对应的输入数据,为了达成「任意两棵树的间隔都为 $y$」的目标, HG 最多可以让多少棵树保持在原来的位置。
输入输出样例
输入样例 #1
1
8 2 3输出样例 #1
3说明
### 样例 1 解释
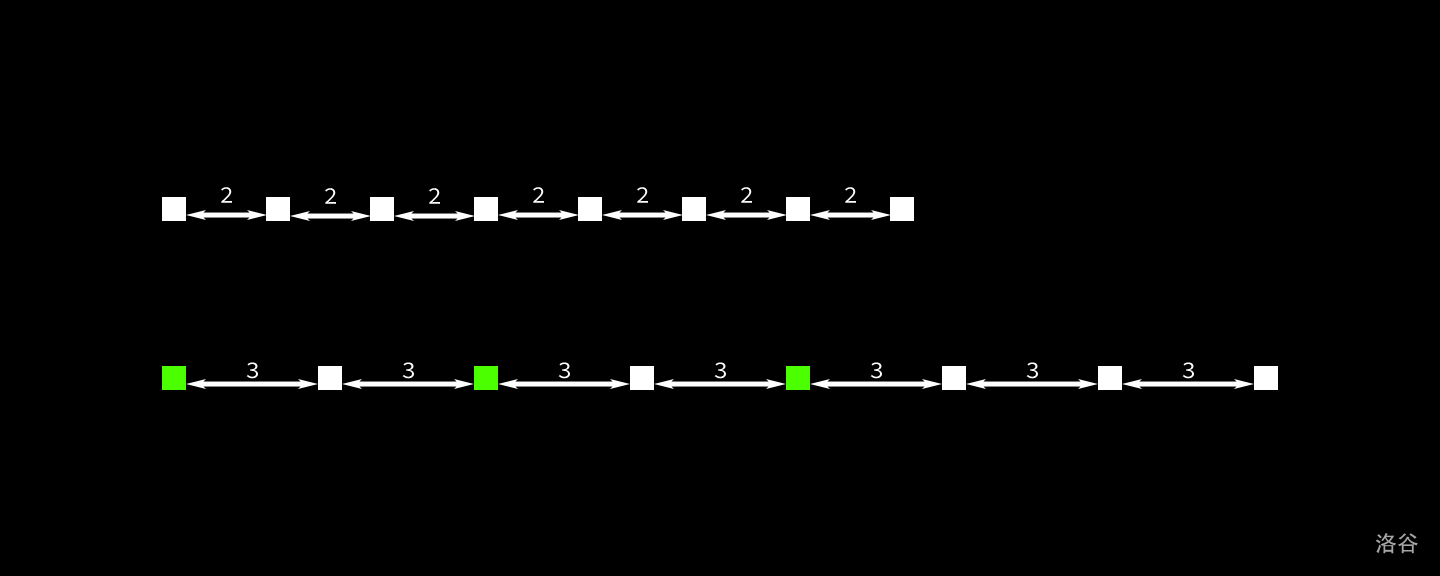
图中的方块代表树。第一行为调整前,第二行为调整后的情况。标出的三个绿色的方块是不需要移动的树,除此之外其他树都需要移动。
### 数据规模与约定
对于 $100\%$ 的数据,保证 $1 \leq T \leq 10 ^ 5$,$1 \leq n \leq 10 ^ {18}$,$1 \leq x < y \leq 10 ^ 9$。