「DTOI-5」校门外的枯树

某天放学，你走出了校门，发现校门外又双叒叕出现了一排树。只不过因为正值寒冬时节，树的叶子都掉光了，树们在寒风中瑟瑟发抖，让人担心它们会不会在某一时刻失去平衡，然后倒下来。

给你校门外的一排 $T$ 棵无向有根树（每棵树的根节点编号均为 $1$），每棵树的每条边有其重量 $m_i$，现在请你算出每棵树的不平衡度 **或** 该树的**每个节点的子树**的不平衡度，好让校方帮忙加固。$\color{white}\sout{\text{不要问我为什么重量的字母是 }m\text。}$ 注意这里的**树的边是有顺序的**，~~你总不可能把树枝掰断然后嫁接到另一个地方吧，这可是枯树啊喂~~。 --- 对于一颗有根树，定义其不平衡度为该树被在根节点与某一叶子节点的一条最短路径分割为左右两部分（两个边集）后（两个边集均不含该最短路径中的边）两部分的边的总重之差的最小值。特别地，**单个点作为树的不平衡度为 $0$**；空边集内边的总重为 $0$。

最开始一行读入两个正整数 $T,k$，$T$ 表示数据组数（即树的总数）。在每组测试数据中，如果 $k=1$，那么你只需要算出整个树的不平衡度即可；如果 $k=2$，**你需要分别对每个节点计算出其子树的不平衡度**。 对于每棵树，第一行读入一个正整数 $n$，$n$ 表示该树内的节点数。 后 $n$ 行，第 $u$ 行描述一个节点，该节点编号为 $u$： - 第一个正整数，表示该点的儿子个数，记为 $x$。 - 后有 $2x$ 个正整数，第 $2i-1$ 个数表示 $u$ 点**从左往右**第 $i$ 个儿子 $v$，第 $2i$ 个数表示连接 $u$ 与 $v$ 的边的重量 $m_{u\leftrightarrow v}$。

输出 $T$ 行： - 如果 $k=1$，第 $i$ 行仅输出一个非负整数表示第 $i$ 棵树的不平衡度。 - 如果 $k=2$，第 $i$ 行输出 $n$ 个非负整数，第 $j$ 个数表示第 $i$ 棵树中的第 $j$ 号节点的子树的不平衡度。

2 1
7
3 3 2 2 114 4 7
3 5 19 6 19 7 514
0
0
0
0
0

11
5 2 4 3 9 8 1 9 7 11 10
0
3 4 8 5 3 7 2
0
1 6 6
0
0
0
1 10 5
0
0

33
2

2 2
7
3 3 2 2 114 4 7
3 5 19 6 19 7 514
0
0
0
0
0

11
5 2 4 3 9 8 1 9 7 11 10
0
3 4 8 5 3 7 2
0
1 6 6
0
0
0
1 10 5
0
0

33 38 0 0 0 0 0
2 0 6 0 0 0 0 0 0 0 0

**【数据范围】** **不捆绑测试**，同一 $\text{Subtask}$ 内每个测试点等分。 $$ %\def\or{\operatorname{or}} %这 arraystretch 咋老是拼错/oh \def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|}\hline \textbf{Subtask}&\sum n\leqslant&k=&\textbf{Special Constraints}&\textbf{Score}\cr\hline \sf1&2\times10^5&1&\bf A&1\cr\hline \sf2&20&1&T=1&5\cr\hline \sf3&5000&1&&5\cr\hline \sf4&10^5&2&\bf B&15\cr\hline \sf5&3\times10^5&1&&30\cr\hline \sf6&2\times10^5&2&\bf A'&4\cr\hline \sf7&3\times10^5&2&&40\cr\hline \end{array} $$ - 特殊性质 $\bf A$ ~~限宽 2.6m~~：保证每棵树只有一个叶子节点（$n\geqslant2$）。 - 特殊性质 $\bf B$ ~~限高 4.5m~~：保证每棵树都为菊花图（根节点有 $n-1$ 个儿子）。 - 特殊性质 $\bf A'$：保证每棵树都是链（每个节点的度数不超过 $2$）。 关于 $\bf A$ 和 $\bf A'$ 的区别：$\bf A'$ 中有可能树的根的度数为 $2$，而 $\bf A$ 中根的度数显然为 $1$。 对于 $100\%$ 的数据，$T \leqslant 4000$，${\color{red}\textbf1}\leqslant n\leqslant 10^5$，$\sum n\leqslant 3\times10^5$，$1 \leqslant m_i \leqslant10^4$，$1\leqslant u, v\leqslant n$，$k\in\{1,2\}$。 --- 叶子节点为没有儿子的节点，即除根节点以外在树中的度为 $1$ 的点。 样例输入中为方便阅读加上了空行，实际数据中没有空行。 **【样例 $\bm1-\bm1$ 解释】** 该树如下图所示，边权即边的重量。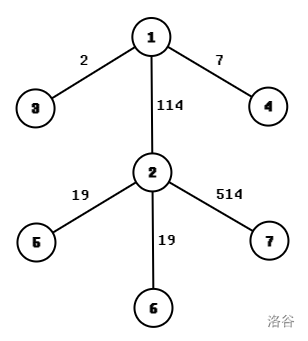  最优解为选择 $1\to2\to7$ 作为分割路径，不平衡度为 ${\large\vert}(2+19+19)-7{\large\vert}=33$。 如果选择 $1\to2\to6$ 作为分割路径，那么两部分的边的总重之差为 ${\large\vert}(2+19)-(7+514){\large\vert}=500$，不为最小值。 $\color{transparent}\sout{不知道你们发现没有\begin{cases}114+2+19+19=154\\114+514+19+19=666\end{cases}}$ **【样例 $\bm1-\bm2$ 解释】** 该树如下图所示。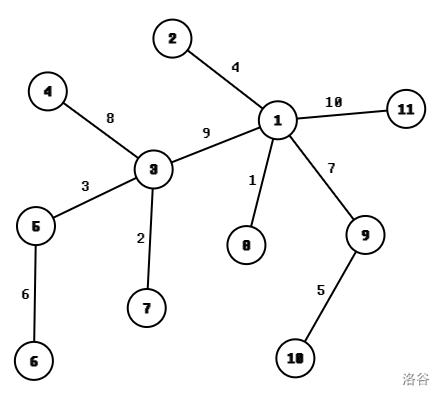  最优解为选择 $1\to7$ 作为分割路径，不平衡度为 ${\large\vert}(4+8+3+6)-(1+7+5+10){\large\vert}=2$。