黄玫瑰
题目描述
给定一张包含 $n$ 个点的简单有向无环图 $G$,点 $i$ 的点权设为 $w_i$,但**点权不是给定的**。
你需要构造一个包含至多 $2\times n$ 个点和恰好 $n$ 条边的有向无环图 $G'$,你需要为 $G'$ 的每条边钦定某个 $w_i$ 作为它的边权,使得 $G'$ 和 $G$ 的**最长路**长度相等。
在 $G$ 中一条路径的长度定义为其中所有点权和,$G'$ 中则为所有边权和。
然而,所有 $w_i$ 都不是给定的,所以你构造的 $G'$ 需要满足:对于任何一种可能的**正数**序列 $[w_1,\ldots,w_n]$,$G$ 和 $G'$ 的最长路长度都要相等。
请构造 $G'$,或说明它不存在。
输入输出格式
输入格式
第一行:两个整数 $n,m$。
接下来 $m$ 行:每行两个整数 $x,y$,表示存在一条点 $x$ 到点 $y$ 的有向边。
输出格式
如果不存在满足题意的 $G'$,则输出一行一个 $-1$。
否则,输出 $n+1$ 行:
第一行:一个整数 $N$,表示你构造的 $G'$ 的点数。
接下来 $n$ 行:每行三个整数 $x,y,z$,表示 $G'$ 中存在一条点 $x$ 到点 $y$ 的边,边权等于 $w_z$。
你需要保证 $0\leq N\leq 2\times n$,$1\leq x,y\leq N$,$1\leq z\leq n$。
若有多种可能的解,任意输出一个即可。
输入输出样例
输入样例 #1
7 8
1 2
1 3
2 3
2 6
3 4
5 2
5 7
6 7
输出样例 #1
7
1 2 1
1 2 5
2 3 2
3 4 3
3 5 6
4 6 4
5 7 7
输入样例 #2
7 8
1 2
2 3
2 6
4 5
4 7
5 3
7 3
7 6
输出样例 #2
-1
说明
**【样例 #1 解释】**
如下图,左为 $G$,右为 $G'$,颜色相同的点/边表示权值相同:
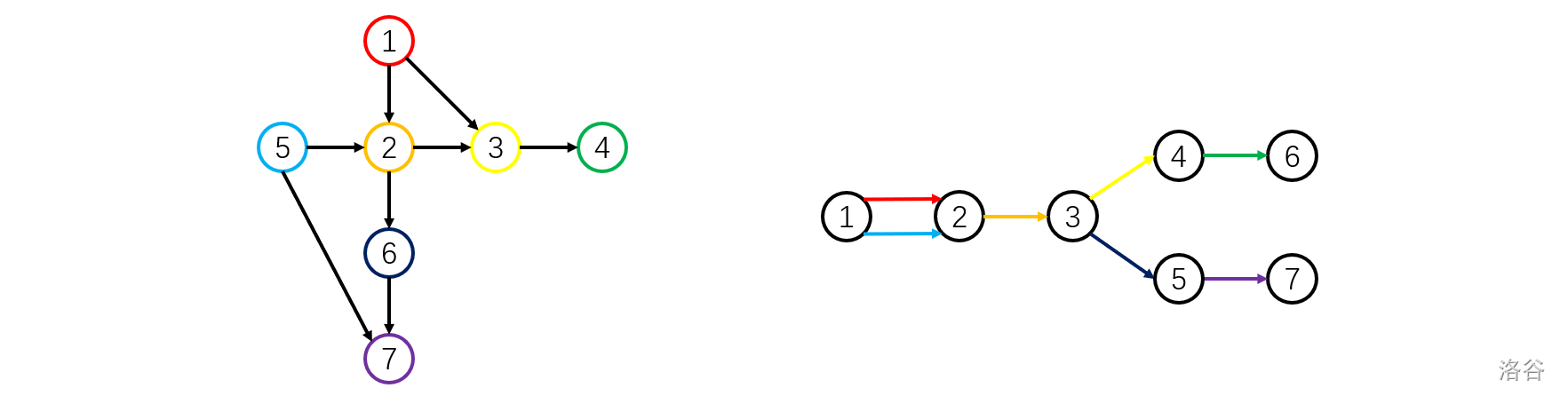
注意这只是一种可能的答案,其他正确的答案也可通过。
---
**【样例 #2 解释】**
下图为 $G$,不存在合法的 $G'$:

---
**【数据范围】**
对于全部数据:$1\leq n\leq 20000$,$1\leq m\leq 3\times 10^5$,$1\leq x,y\leq n$,保证给定的图无环且无重边。
| 子任务编号 | $n\leq$ | $m\leq$ | 特殊性质 | 分值 |
| :----------------: | :-----: | :------------: | :---------------------------: | :--: |
| $\text{Subtask 1}$ | $5000$ | $4999$ | $m=n-1$,每个点入度不超过 $1$ | $18$ |
| $\text{Subtask 2}$ | $5000$ | $4999$ | $m=n-1$,每个点出度不超过 $1$ | $19$ |
| $\text{Subtask 3}$ | $20$ | $50$ | 无 | $20$ |
| $\text{Subtask 4}$ | $5000$ | $10000$ | 无 | $21$ |
| $\text{Subtask 5}$ | $20000$ | $3\times 10^5$ | 无 | $22$ |
---
