[NAPC-#1] rStage5 - Hard Conveyors

**本题新增两组 hack 数据。** ---  更硬，所以可能就更脆，所以更容易被击破（确信）。 您只花了两个小时就秒掉了正城 s1~s10，来秒逆城了。

**本题与 Stage5 的区别是合法路径定义不同**（简要题意中加粗部分不同）。~~（其实还有：样例不同，数据不同，部分分不同。）~~ ### 【简要题意】 给定一棵 $n$ 个节点的无根树以及树上的 $k$ 个关键节点，边有边权（即边的长度）。$q$ 次询问，每次给出 $s,t$，问从 $s$ 到 $t$ 且经过**至少一个**关键节点的路径的最短长度。

第一行三个正整数 $n, q, k$，表示树的节点个数，询问次数和关键节点个数。 接下来 $n-1$ 行，每行三个正整数 $u, v, w$，表示树中存在边 $(u, v)$，边权为 $w$。保证输入构成一棵树。 接下来一行 $k$ 个两两不同的正整数，表示关键节点的编号。 接下来 $q$ 行，每行两个正整数 $s, t$，表示一次询问。

对于每次询问输出一行一个非负整数，表示此次询问的最短合法路径长度。 注意，合法路径可以不经过任何边，此时路径长为 $0$。

7 6 2
1 2 3
1 3 5
3 4 2
3 5 4
2 6 1
1 7 1
2 3
2 3
2 1
7 1
4 5
6 6
2 2

8
3
7
6
2
0

### 【数据范围】 upd at `2023-6-25`：新增了两组 hack 数据，将其置于 $\text{Sub}\textsf6$ 中，不记分数。 **本题采用捆绑测试。** $$ \def\r{\cr\hline} \def\None{\text{None}} \def\arraystretch{1.5} \begin{array}{c|c|c|c} \textbf{Subtask} & \text{测试点编号} & \textbf{Sp. Constraints} & \textbf{Score}\r \textsf1&1\sim2 & k=n & 5 \r \textsf2&16\sim20 &k=1,n\leqslant10^3,q\leqslant10^3 & 15 \r \textsf3&21\sim25 & n\leqslant10^3,q\leqslant10^3 & 15 \r \textsf4&3\sim7 & q=1 & 15 \r \textsf5&8\sim15 & - & 50 \r \textsf6&26\sim27 & - & 0 \r \end{array} $$ 对于 $100\%$ 的数据，$1\leqslant n\leqslant 10^5$，$1\leqslant q\leqslant 10^5$，$1\leqslant k\leqslant n$，$1\leqslant w\leqslant 10^4$，$1\leqslant u,v,s,t\leqslant n$。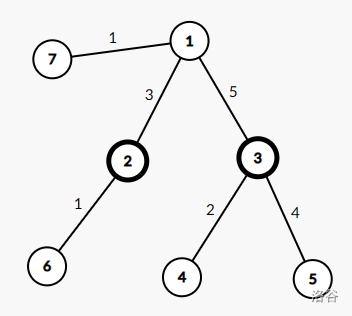 ### 【样例解释 #1】  图中加粗节点表示关键点。 对于每组询问，以下为一种最优路径（最优路径可能有多条）： 1. $2\to1\to3$。 2. $2\to1$。 3. $7\to1\to2\to1$。 4. $4\to3\to5$。 5. $6\to2\to6$。 6. $2$（合法路径可以不经过任何边，此时路径长为 $0$）。