『GROI-R2』 Beside You

記憶の森 始まりの謎 いつか この未知の果てに告げ知らせて ——江口孝宏《Beside You》

我相信所有读过这一段剧情的人都不想让别人也经历一样的痛苦，但是坦尼尔还是只能消失，对吗？ 坦尼尔最后留下了一棵以 $1$ 为根的有根树，在树的每个结点上，都有一个记忆碎片。有的碎片表示着一个世界记忆的开始，而另外的碎片表示着一个世界记忆的终结。 这时，树上飞来了一只蝴蝶~~モリモリあつし~~。蝴蝶在树上飞舞的过程中，经过了一些结点。爱丽丝能确定蝴蝶经过的结点个数至少有 $2$ 个，但是她忘记了具体的点数。 爱丽丝发现，蝴蝶经过的所有点都是互相连通的。当她把目光朝向每一条经过点数大于 $1$ 的从连通块**深度最小的结点**通往**连通块的任意一个叶子结点**（一个点是连通块的叶子结点，当且仅当它在树上没有子结点，或者它在树上的任意子结点均不在该连通块内）的简单路径时，她发现这些路径上的记忆都是完整的。爱丽丝认为一条路径上的记忆是完整的，当且仅当这条路径上既没有出现一个世界的记忆**没开始就结束**（路径中途在没有未结束的记忆的时候，出现了表示记忆终结的碎片）的情况，也没有出现一个世界的记忆**开始之后没有终结**（路径结束之后还有没结束的记忆）的情况。 可惜她已经遗忘了蝴蝶经过了哪些点，所以你需要告诉她蝴蝶**最多**可能经过多少点。 **形式化题面** 给定一棵以 $1$ 为根的 $n$ 个节点的树 $T=(V,E)$，每个节点上的点权 $c_i$ 为一个**左括号或一个右括号**，节点编号为 $1\sim n$。 我们定义点集 $V'\subseteq V$ 合法，当且仅当 $|V'|>1$（**即 $V'$ 的大小大于 $1$**） 且 $\forall u,v \in V'$，从 $u$ 到 $v$ 的简单路径只经过 $V'$ 中的点。 同时我们定义 $E'\subseteq E$ 为能使得 $\forall u,v \in V'$，从 $u$ 到 $v$ 的简单路径，只经过 $E'$ 中的边的大小最小的边集。 定义一个合法点集 $V'$ 的根为 $V'$ 中深度最小的结点。 定义 $u$ 为合法点集 $V'$ 的叶子节点，当且仅当 $u$ 不是 $V'$ 的根，且满足 $v \in V', (u,v) \in E'$ 的 $v$ 的数量为 $1$。 求一个合法点集 $S$，**满足其根节点到其任意一个叶子的路径上，每个点的点权顺次相接为一个合法的括号序列**，并**最大化** $|S|$。 我们通过如下规则定义一个合法的括号序列： - 空串（即长度为 $0$ 的串）是一个合法的括号序列。 - 若串 $\text{A,B}$ 都是合法的括号序列，则字符串 $\text{AB}$ （即将字符串 $\text{A}$ 与 $\text{B}$ 按顺序拼接起来）也是合法的括号序列。 - 若串 $\text{A}$ 是合法的括号序列，则字符串 $\text{(A)}$ 是一个合法的括号序列。 你需要输出符合要求的最大 $|S|$。

第一行输入一个正整数 $n$ 表示树上结点个数。 第二行输入一个长度为 $n$ 的字符串 $c$。$c_i$ 为 ``(`` 表示这个结点上有一个标志着记忆开始的碎片，$c_i$ 为 ``)`` 表示这个结点上有一个标志着记忆终结的碎片。 接下来 $n-1$ 行，每行输入两个正整数 $u,v$，表示结点 $u,v$ 之间有一条边。

输出一行一个整数，表示答案。

3
())
1 2
1 3

3

8
()))())(
1 2
1 3
3 4
3 5
3 6
5 7
2 8

5

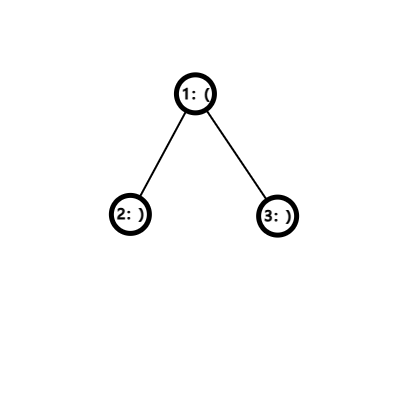
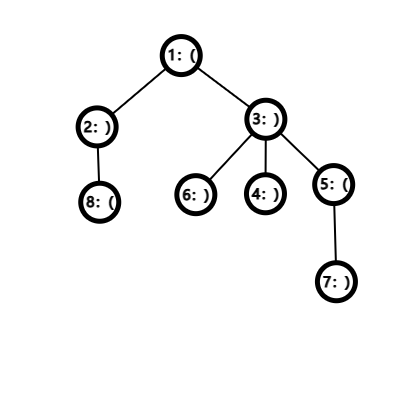
**样例解释**  蝴蝶经过的最大合法点集 $S$ 为 $\{1,2,3\}$。  蝴蝶经过的最大合法点集 $S$ 为 $\{1,2,3,5,7\}$。 **数据范围** **本题采用捆绑测试**。 | $\text{Subtask}$ | $n\le$ | 特殊性质 | 分值 | | :-----------: | :-----------: | :-----------: | :-----------: | | $1$ | $20$ | | $5$ | | $2$ | $3000$ | | $20$ | | $3$ | $5\times10^5$ | $\text{A}$ | $15$ | | $4$ | $5\times10^5$ | $\text{B}$ | $10$ | | $5$ | $2\times10^5$ | | $15$ | | $6$ | $5\times10^5$ | | $35$ | 特殊性质 $\text{A}$：保证树退化成一条链（不保证 $1$ 号节点为其一个端点）。 特殊性质 $\text{B}$：保证原树上任意结点到叶子的路径上右括号数量不少于左括号数量。 对于 $100\%$ 的数据满足 $1\le n\le 5\times 10^5$，$1\le u,v \le n$，$c_i$ 为 ``(`` 或 ``)``。