[ICPC2020 Shanghai R] Sky Garden

Prof. Du 和 Prof. Pang 计划在 Allin 城周围建立一个天空花园。在花园中，将有一个由直路和圆弧路组成的植物迷宫。 在植物迷宫的蓝图上，Prof. Du 画了 $n$ 个圆来表示所有的圆弧路，所有的 $n$ 个圆的圆心均为 $(0,0)$，第 $i$ 个圆的半径为 $i$。 同时，Prof. Pang 在蓝图上画了 $m$ 条直线，表示所有的直路。这 $m$ 条直线将所有的圆均分为 $2m$ 份。 假定集合 $Q$ 是所有 $n+m$ 条路的集合，集合 $P$ 是 $Q$ 中任意两条不相同的路的交点的集合。请注意，每条直线和每个圆有两个交点。 对于任意两个不同的点 $a\in P$，$b\in P$，定义 $\operatorname{dis}(\{a,b\})$ 为从点 $a$ 走到点 $b$ 的最短距离。对于所有 $\{a,b\} \subseteq P$，计算 $\operatorname{dis}(\{a,b\})$ 的和。

Prof. Du and Prof. Pang plan to build a sky garden near the city of Allin. In the garden, there will be a plant maze consisting of straight and circular roads. On the blueprint of the plant maze, Prof. Du draws $n$ circles indicating the circular roads. All of them have center $(0, 0)$. The radius of the $i$-th circle is $i$. Meanwhile, Prof. Pang draws $m$ lines on the blueprint indicating the straight roads. All of the lines pass through $(0, 0)$. Each circle is divided into $2m$ parts with equal lengths by these lines. Let $Q$ be the set of the $n+m$ roads. Let $P$ be the set of all intersections of two different roads in $Q$. Note that each circular road and each straight road have two intersections. For two different points $a\in P$ and $b\in P$, we define $dis(\{a, b\})$ to be the shortest distance one needs to walk from $a$ to $b$ along the roads. Please calculate the sum of $dis(\{a, b\})$ for all $\{a, b\}\subseteq P$.

The only line contains two integers $n,m~(1\le n,m\le 500)$.

Output one number -- the sum of the distances between every pair of points in $P$. Your answer is considered correct if its absolute or relative error does not exceed $10^{-6}$.

1 2

14.2831853072

2 3

175.4159265359

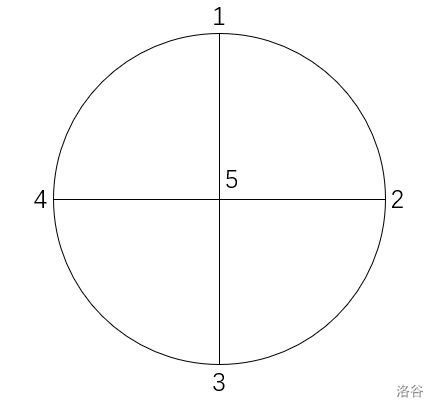
 $dis(p_1, p_2)=dis(p_2, p_3)=dis(p_3, p_4)=dis(p_1, p_4)=\frac{\pi}{2}$ $dis(p_1, p_5)=dis(p_2, p_5)=dis(p_3, p_5)=dis(p_4, p_5)=1$ $dis(p_1, p_3)=dis(p_2, p_4)=2$