[ICPC2020 Shanghai R] Traveling Merchant

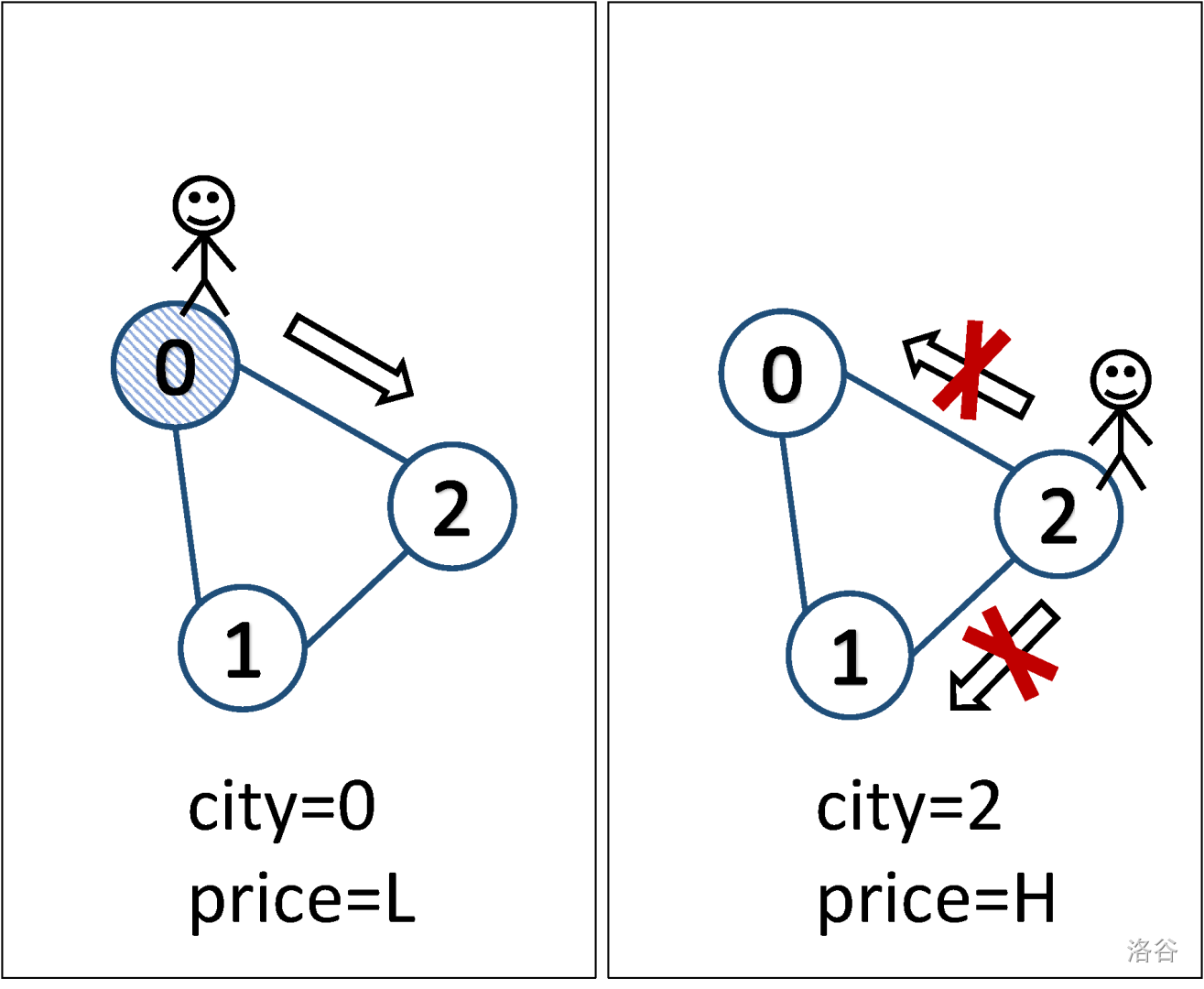
### 题目描述 劳伦斯先生是一位在不同城市转售商品的旅行商人。基本地，为了赚钱，他需要以低价买进商品，再以高价卖出。现在请你为他规划一条可以一直盈利的旅行路线。 简单地说，假设有 $n$ 座城市，标号为 $0$ 到 $n-1$ ，以及 $m$ 条连接特定两座城市的路，劳伦斯先生可以通过这些路到访每座城市。最初劳伦斯先生位于第 $0$ 座城市，并且对于城市 $i$ 都有一个起始价格 $c_i$ 。根据市场规律，当他从城市 $i$ 来到相邻的城市 $j$ 时（当且仅当城市 $i$ 与城市 $j$ 之间有路径相连时，才称 $i$ 与 $j$ 为相邻城市），城市 $i$ 的价格状况会发生变化（高价会变成低价，低价也可能变成高价）。而因为一些原因（比如商品的新鲜程度，旅行费用，税务等），他**必须**： - 从城市 $0$ 出发并在城市 $0$ 购买一些商品。保证城市 $0$ 的起始价格很**低**。 - 每当他到达一座城市后，他**必须**售卖**或**购买一些商品。 - 若他在城市 $i$ 购买了商品，他就必须去一座与 $i$ 相邻且价格 $c_j$ **高于** $c_i$ 的城市 $j$ ，并在那里卖掉手中来自城市 $i$ 的商品。 - 若他在城市 $i$ 售卖了商品，他就必须去一座与 $i$ 相邻且价格 $c_j$ **低于** $c_i$ 的城市 $j$，并在那里购买一些商品。 因此，最终路径会始终重复 ``低价购入`` 和 ``高价卖出`` 。 一条无尽的盈利路线由无尽的城市序列 $p_0,p_1 \dots$ 组成。其中，城市 $p_i$ 与城市 $p_{p+1}$ 之间有路径相连，$p_0 = 0$，且价格高低是交替循环的，也就是说当 $k \ge 0$ 时，城市 $p_{2k}$ 的价格 $c_{p_{2k}} = \text{Low}$ (要在这个城市购买商品) 而相邻城市 $p_{2k+1}$ 的价格 $c_{p_{2k+1}} = \text{Hign}$ (要在这个城市卖出商品)。 **注意**：$c_{p_i}$ 是 **到达** 城市 $p_i$ 时的价格，而当他第二次到达城市 $p_i$ 时，这个价格可能会因为市场规律而变化。 你需要写一个程序，判断是否有这样一条永远盈利的路径存在。 ### 输入格式 输入有多组数据。所有数据的第一行是一个整型 $T$ 表示数据组数。每组数据的第一行是两个整型 $n$ 和 $m$，表示城市的数量和道路的数量。 每组数据的第二行是一个长度为 $n$ ，由 $H$ 或 $L$ 组成的字符串 $c$ 。字符串 $c$ 的第 $i$ 个字符若为 $H$，则表示城市 $i$ 的起始价格 $c_i$ **高**，反之若为 $L$ 则表示城市 $i$ 的起始价格 $c_i$ **低**。 接下来 $m$ 行，每行输入一组 $u_i$ 和 $v_i$ ，表示一条连接城市 $u_i$ 和城市 $v_i$ 的双向路径。 所有数据中 $n$ 的总和不超过 $200,000$ ，$m$ 的总和也不超过 $200,000$ 。对于每组数据，$c_i\in\{\text{H}, \text{L}\}$ 对应每个 $i\in\{0, \dots, n-1\}$ ，保证 $c_0$ 总为 $L$ 。保证对于每个 $i\in\{1,\dots,m\}$ ，都有 $0 \leq u_i,v_i < n$ 且 $u_i \neq v_i$ 。保证每两座城市之间只有一条路径相连。 ### 输出格式 对于每组数据，输出一行 ``yes`` 或者 ``no`` ，表示是否存在一条无尽的盈利路径。

Mr. Lawrence is a traveling merchant who travels between cities and resells products. Basically, to earn from it, he needs to buy products at a very low price and sell them at a higher price. Your task is to tell him whether there exists an endless traveling path that can earn money all the time. To make things simple, suppose there are $n$ cities named from $0$ to $n-1$ and $m$ undirected roads each of which connecting two cities. Mr. Lawrence can travel between cities along the roads. Initially he is located at city $0$ and each of the city $i$ has a starting price $c_i$, either $\text{Low}$ or $\text{High}$. Due to the law of markets, the price status at city $i$ will change (i.e. $\text{High}$ price will become $\text{Low}$ price, or vice versa) after he departs for a neighboring city $j$ from $i$. (City $j$ is a neighboring city of city $i$ when one of the $m$ roads connects city $i$ and city $j$.) For some reasons (e.g. product freshness, traveling fee, tax), he $\textbf{must}$: - Start at city $0$ and buy products at city $0$. It is guaranteed that $c_0$ is $\text{Low}$. - When he arrives some city, he either sells products or buys products. It is not allowed for him to do nothing before he leaves the city. - After buying products at some city $i$, he must travel to some neighboring city $j$ whose price $c_j$ is $\text{High}$ and sell the products at city $j$. - After selling products at some city $i$, he must travel to some neighboring city $j$ whose price $c_j$ is $\text{Low}$ and buy the products at city $j$. As a result, the path will look like an alternation between ``buy at low price'' and ``sell at high price''. An endless earning path is defined as a path consisting of an endless sequence of cities $p_0, p_1,\dots$ where city $p_i$ and city $p_{i+1}$ has a road, $p_0=0$, and the price alternates, in other words $c_{p_{2k}}=\text{Low}$ (indicates a buy-in) and $c_{p_{2k+1}}=\text{High}$ (indicates a sell-out) for $k\geq0$. Please note here $c_{p_i}$ is the price when $\textbf{arriving}$ city $p_i$ and this value may be different when he arrives the second time. Your task is to determine whether there exists any such path.

There are several test cases. The first line contains a positive integer $T$ indicating the number of test cases. Each test case begins with two positive integers $n$ and $m$ indicating the number of cities and the number of roads. The next line is a string $c$ of length $n$ containing `H' or `L'. The $i$-th ($0\le i<n$) charactor of $c$ is $H$ if the starting price $c_i$ at city $i$ is $\text{High}$. The $i$-th ($0\le i<n$) charactor of $c$ is $L$ if the starting price $c_i$ at city $i$ is $\text{Low}$. The $i$-th line ($1\le i\le m$) of the following $m$ lines contains two different cities $u_i$ and $v_i$, indicating a road between $u_i$ and $v_i$. The sum of the values of $n$ over all test cases is no more than $200,000$. The sum of the values of $m$ over all test cases is no more than $200,000$. For each test case, $c_i\in\{\text{H},\text{L}\}$ holds for each $i\in \{0, \ldots, n-1\}$. $c_0$ is always $L$. $0\leq u_i,v_i<n$ and $u_i\neq v_i$ hold for each $i\in \{1,\ldots, m\}$. No two roads connect the same pair of cities.

For each test case, output a line of ``yes`` or ``no``, indicating whether there exists an endless earning path.

2
4 4
LHLH
0 1
1 2
1 3
2 3
3 3
LHH
0 1
0 2
1 2

yes
no

In the first sample test case, the endless earning path is $0\rightarrow 1\rightarrow 2\rightarrow 3\rightarrow 1\rightarrow 2\rightarrow 3\rightarrow \dots$. In the illustration, cities with $\text{Low}$ price are filled with stripe.  In the second sample test case, Mr. Lawrence can only make one move from city $0$ and after that all cities will have $\text{High}$ price. Thus, no further moves can be made.