[ICPC2018 Qingdao R] Sequence and Sequence

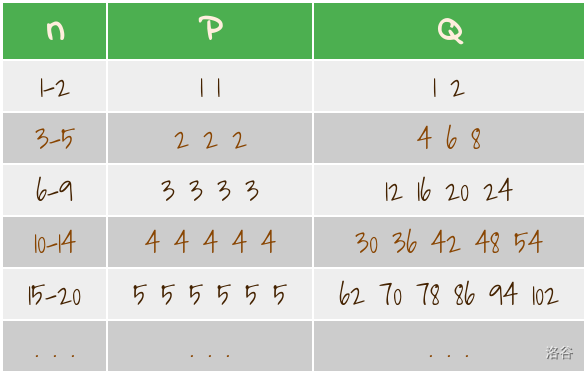
### 题目描述 考虑下列两个序列 $P$ 和 $Q$。我们用 $P(i)$ 表示序列 $P$ 中的第 $i$ 个元素，用 $Q(i)$ 表示序列 $Q$ 中的第 $i$ 个元素： - 序列 $P$ 是一个**已排序的**序列，其中，对于所有 $k \in \mathbb{Z^+}$，$k$ 在序列 $P$ 中出现 $(k+1)$ 次（$\mathbb{Z^+}$ 为正整数集）。也就是说，$P = \{1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, \dots \}$ - 序列 $Q$ 可以由以下方程导出： $$\begin{cases} Q(1) = 1 & \\ Q(i) = Q(i-1) + Q(P(i)) & \text{if } i > 1 \end{cases}$$ 也就是说，$Q = \{1, 2, 4, 6, 8, 12, 16, 20, 24, 30, 36, 42, 48, 54, 62, \dots \}$。  给定一个正整数 $n$，请计算 $Q(n)$ 的值。 ### 输入格式 本题的测试点包含多组测试数据。 第一行输入包含一个整数 $T$ （$10^4$ 左右），表示测试数据的数量。对于每组测试数据： - 第一行（也是唯一一行）包含一个整数 $n$ （$1 \le n \le 10^{40}$）。 ### 输出格式 对于每组测试数据，输出一行，包含一个整数，表示 $Q(n)$ 的值。

Consider the following two sequences $P$ and $Q$. We denote $P(i)$ as the $i$-th element in sequence $P$, and $Q(i)$ as the $i$-th element in sequence $Q$: - Sequence $P$ is a $\textbf{sorted}$ sequence where for all $k \in \mathbb{Z^+}$, $k$ appears in sequence $P$ for $(k+1)$ times ($\mathbb{Z^+}$ is the set of all positive integers). That is to say, $P = \{1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, \dots \}$ - Sequence $Q$ can be derived from the following equations: $$\begin{cases} Q(1) = 1 & \\ Q(i) = Q(i-1) + Q(P(i)) & \text{if } i > 1 \end{cases}$$ That is to say, $Q = \{1, 2, 4, 6, 8, 12, 16, 20, 24, 30, 36, 42, 48, 54, 62, \dots \}$  Given a positive integer $n$, please calculate the value of $Q(n)$.

There are multiple test cases. The first line of the input contains an integer $T$ (about $10^4$), indicating the number of test cases. For each test case: The first and only line contains an integer $n$ ($1 \le n \le 10^{40}$).

For each test case output one line containing one integer, indicating the value of $Q(n)$.

4
10
100
1000
987654321123456789

30
2522
244274
235139898689017607381017686096176798