[ICPC2018 Qingdao R] Mirror

### 题目描述 在一个无限二维平面上包含一个不透明障碍物和一个单面镜子。障碍物被表示为一个三角形，而镜子被表示为一个从点 $(x_{m,1}, y_{m,1})$ 指向 $(x_{m,2}, y_{m,2})$ 的有方向的线段，线段的右侧是反射面。 有 $m$ 个石头位于点 $(x_1,y_1)$，DreamGrid 希望将所有石头移动到点 $(x_2,y_2)$。需要满足以下条件： DreamGrid 每次只能携带一个石头。 一旦 DreamGrid 拿起一个石头，他只能将其放置在点 $(x_2,y_2)$。 设 $L$ 为 DreamGrid 走过的路径，对于路径上的每一个点 $p$，DreamGrid 必须能直接或通过镜子看到所有的石头。 **注意：** 如果视线的某部分在障碍物内（视线穿过障碍物的点或边界是允许的），则认为 DreamGrid 无法通过这条视线看到石头。 如果镜子的一个端点在视线上，认为 DreamGrid 既可以在镜子中看到石头，也可以透过镜子看到石头。 反射过程遵循物理规律：入射角等于反射角。入射光线和反射光线在镜子的同一侧。 如果视线与镜子平行，则不发生反射，镜子不被视为障碍物。 DreamGrid 不能移动进入障碍物，但可以在障碍物的边缘或顶点上移动。 DreamGrid 不能穿过镜子移动，但可以在镜子上移动。注意，如果 DreamGrid 在镜子的线段上（不包括两个端点），他只能看到他来的那一侧，并且不能透过镜子看到。 DreamGrid 想要知道移动所有石头从 $(x_1,y_1)$ 到 $(x_2, y_2)$ 的最短距离。 ### 输入格式 输入包括多个测试用例。第一行是一个整数 $T$（大约 100），表示测试用例的数量。对于每个测试用例： 第一行包含一个整数 $m$（$1 \le m \le 10^6$），表示石头的数量。 第二行包含四个整数 $x_1$, $y_1$, $x_2$ 和 $y_2$，表示起始点和目标点。 第三行包含四个整数 $x_{m,1}$, $y_{m,1}$, $x_{m,2}$ 和 $y_{m,2}$，表示镜子的坐标。 接下来的 $3$ 行，每行包含两个整数 $x_i$ 和 $y_i$，表示障碍物顶点的坐标。 所有坐标的绝对值不超过 $100$。起始点和目标点都在障碍物和镜子之外。镜子和障碍物没有公共点。 保证没有三个点是共线的。 ### 输出格式 输出对于每个测试用例，输出一个实数表示最短距离，如果 DreamGrid 无法在约束条件下移动所有石头，则输出 $-1$。 如果你的答案的绝对误差或相对误差小于 $10^{-6}$，则认为你的答案是正确的。

There is a non-transparent obstacle and a single-sided mirror in an infinite two-dimensional plane. The obstacle can be represented as a triangle and the mirror can be represented as a $\textbf{directional}$ line segment pointing from $(x_{m,1}, y_{m,1})$ to $(x_{m,2}, y_{m,2})$, with the right side being reflective. There are $m$ stones at point $(x_1,y_1)$ and DreamGrid would like to move all the stones to point $(x_2,y_2)$. The following constraints must be satisfied: - DreamGrid can only carry one stone each time. - Once DreamGrid picks up a stone, he can only put it down at point $(x_2,y_2)$. - Let $L$ be the path DreamGrid walked, then for each point $p$ on $L$, DreamGrid should see all the stones directly or through the mirror. Note that: - If some part of the line vision is inside the obstacle (it's ok that the line vision passes a point or edge of the obstacle), it's considered, that DreamGrid cannot see the stone with this line of vision. - If one of the two endpoints of the mirror is on the line of vision, it's considered, that DreamGrid can see the stone both in the mirror and through the mirror. - The reflection process is governed by laws of physics --- the angle of incidence is equal to the angle of reflection. The incident ray is in the same half-plane as the reflected ray, relative to the mirror. - If the line of vision is parallel to the mirror, reflection doesn't take place, and the mirror isn't regarded as an obstacle. - DreamGrid cannot move into the obstacle but can move on the edges or the vertices of the obstacle. - DreamGrid cannot move through the mirror but can move on the mirror. Note that if DreamGrid is on the line segment of the mirror other than the two endpoints, he can only see the side he comes from, and cannot see through the mirror. DreamGrid would like to know the shortest distance to move all stones from $(x_1,y_1)$ to $(x_2, y_2)$.

There are multiple test cases. The first line of input is an integer $T$ (about 100), indicates the number of test cases. For each test case: The first line contains one integer $m$ ($1 \le m \le 10^6$), indicating the number of stones. The second line contains four integers $x_1$, $y_1$, $x_2$ and $y_2$, indicating the start point and the target point. The third line contains four integers $x_{m,1}$, $y_{m,1}$, $x_{m,2}$ and $y_{m,2}$, indicating the coordinates of the mirror. Each of the next $3$ lines has two integers $x_i$ and $y_i$, indicating the coordinates of the vertices of the obstacle. All the coordinates will not exceed $100$ in absolute value. Both the start point and target point are outside the obstacle and the mirror. The mirror and the obstacle have no points in common. It is guaranteed that no three points are collinear.

For each test case, output a real number indicating the shortest distance, or output $-1$ if DreamGrid cannot move all the stones under the constraints. Your answer will be considered correct if and only if the absolute error or relative error of your answer is less than $10^{-6}$.

2
2
-2 0 2 0
-3 3 3 3
0 1
-3 -2
3 -2
2
-2 0 2 0
-3 3 -1 3
0 1
-3 -2
3 -2

13.416407864999
-1

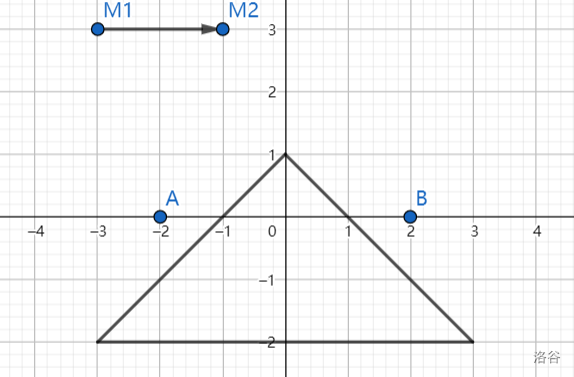
We now welcome our special guest Mashiro, who heartily donates this problem to our problemset, to explain the sample test cases for us using her sketch book.    $\textit{(Image from pixiv. ID: 32084305)}$ In the figures above, we indicate the start point as point $A$ and the target point as point $B$. The mirror is indicated by the line segment pointing from $M1$ to $M2$, with the right side being reflective. For the first sample test case, the optimal path is $A \to C \to B \to C \to A \to C \to B$. For the second sample test case, as DreamGrid cannot see $A$ from $B$, it's impossible to move all the two stones from $A$ to $B$ while following the constraints in the problem description.