『PG2』弯曲半平面直线同向图最大流

若能将有向图 $G=(V,E)$ 画在平面上，使得点在一条直线上，任意两条边（可以为弯曲的弧线）仅在重合顶点处相交，且边上的所有点都在直线同侧，且每条边的起点到终点的射线的方向相同，则称 $G$ 是弯曲半平面直线同向图。对于一个弯曲半平面直线同向图给定 $n$ 个点，$m$ 条有向边，给定每条边的容量，求从点 $s$ 到点 $t$ 的最大流。

第一行包含四个正整数 $n$、$m$、$s$、$t$，用空格分隔，分别表示点的个数、有向边的个数、源点序号、汇点序号。 接下来 $m$ 行每行包含三个正整数 $u_i$、$v_i$、$c_i$，用空格分隔，表示第 $i$ 条有向边从 $u_i$ 出发，到达 $v_i$，容量为 $c_i$。

一个整数，表示 $s$ 到 $t$ 的最大流。

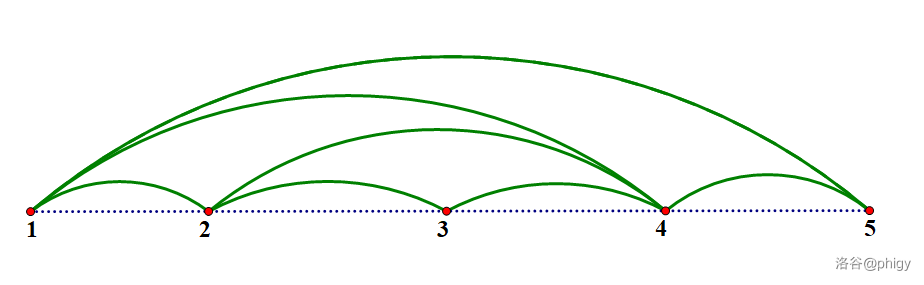
5 7 1 5
1 2 1
2 3 1
3 4 1
4 5 1
2 4 1
1 4 1
1 5 1

2

无重边自环。 对于 $30\%$ 的数据 $n\leq 10^3$。 对于 $70\%$ 的数据 $n\leq 10^5$。 对于 $100\%$ 的数据 $2\leq n\leq 10^6$，$1\leq m\leq \min\{2\times 10^9,\dfrac{n(n-1)}{2}\}$，$1\leq c\leq 10^{12}$，$s\neq t$。 ### 样例解释 1