如何优雅地尺规做正五角星
Carey_chen
·
·
算法·理论
这是一篇关于如何优雅地完成劳技作业尺规作正五角星的文章。
背景
劳技课作业要求做一个木工的正五角星。
先规约一下问题:如果能够尺规作正五边形,那么可以将正五边形的顶点两两相连后得到正五角星。
因此只要讨论如何作正五边形即可。
结论
若正五边形的外接圆半径为 r ,则这个正五边形的边长的长度等于直角边分别为 r 和 \frac{\sqrt 5 -1}{2}r 的直角三角形的斜边边长。
需要用到的符号与定理
勾股定理
在 Rt\triangle MNO 中,有:
### 三角函数间的关系
$$\sin^2 \theta + \cos^2 \theta = 1$$ 。
证明:
在 $Rt\triangle MNO$ 中,有:
\begin{split}
\sin^2 \theta + \cos^2 \theta &= \frac{a^2}{c^2} + \frac{b^2}{c^2} \
&= \frac{a^2 + b^2}{c^2} \
&= \frac{c^2}{c^2} \
&= 1 \
\end{split}
### 余弦定理
其实是勾股定理的扩展。
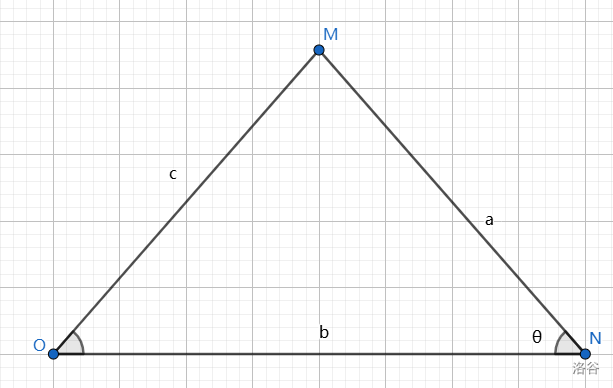
在**任意三角形**中有:
$$a^2+b^2-2ab\cos\theta=c^2
五边形的证明
在一个正五边形的外接圆中,圆心角(以圆心为顶点的的角)\alpha = 72° ,设其半径为 r 。
$∴$ $AP$ 为 $∠\alpha$ 的角平分线,且 $AP$ 垂直平分 $LK$ 。
$∴
LK &= 2LP \\
&= 2 LA \sin (\frac{\alpha}{2}) \\
&= 2 LA \sin (36°) \\
&= 2r \sin (36°) \\
\end{split}
因此求出 \sin (36°) 即可。
新图:
在一个含有 36° 的等腰三角形中,做 ∠BAC 的角平分线,可证明 AC=AD=DB 且 \triangle ADC \sim \triangle BAC。
因此有:
\begin{split}
\frac{AB}{AD} &= \frac{AC}{DC} \\
\frac{AB}{AC} &= \frac{AC}{AB-AC} \\
AB^2 - AB \cdot AC -AC^2 &= 0\\
\end{split}
利用二次方程求根公式得:
AB = \frac{\sqrt 5+1}{2} AC
根据余弦定理:
\begin{split}
AC^2 &= AB^2 + BC^2 - 2AB\cdot BC\cdot\cos 36° \\
AC^2 &= 2AB^2(1 - \cos 36°)
\end{split}
把:AB = \frac{\sqrt 5+1}{2} AC 带入:
\begin{split}
AC^2 &= 2AB^2(1 - \cos 36°) \\
AC^2 &= 2(\frac{\sqrt 5+1}{2} AC)^2(1 - \cos 36°) \\
AC^2 &= AC^2(\sqrt 5+3)(1 - \cos 36°) \\
(\sqrt 5+3)(1 - \cos 36°) &= 1 \\
1 - \cos 36° &= \frac{3 - \sqrt 5}{4} \\
\cos 36° &= \frac{\sqrt 5 + 1}{4}
\end{split}
又因为:
\sin^2 36° + \cos^2 36° = 1
所以:
\sin 36° = \frac{\sqrt{10-2\sqrt{5}}}{4}
回到这张图:
LK &= 2r \sin (36°) \\
&= \frac{\sqrt{10-2\sqrt{5}}r}{2} \\
\end{split}
$∴$ 结论得证。
## 怎么画
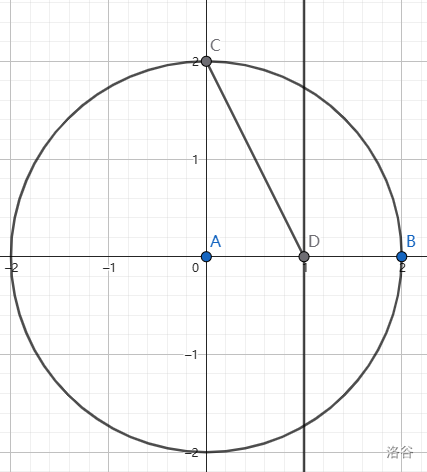
在平面直角坐标系中,$A$ 与原点重合,先在 $x$ 轴的正半轴任取一点 $B$,以 $A$ 点为圆心,画一个以 $AB$ 为半径的圆,作 $AB$ 的垂直平分线,交 $AB$ 于 $D$。
令 $C$ 点为 $y$ 轴的正半轴与圆的交点,连接 $CD$。
此时 $CD = \sqrt 5 AB$ 。
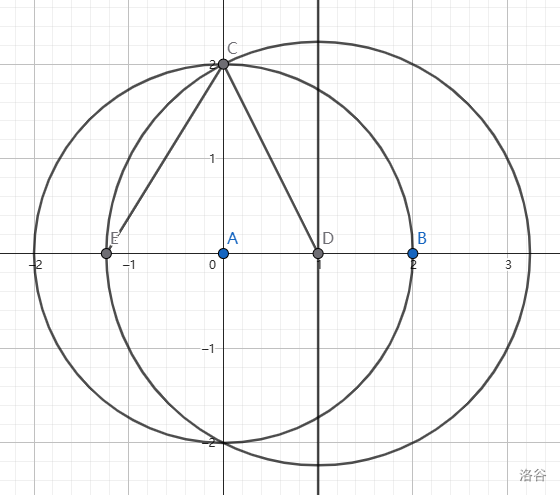
再以 $D$ 点为圆心,画一个以 $CD$ 为半径的圆,交 $y$ 轴的负半轴于点 $E$,连接 $CE$ 。
此时 $AE = \frac{\sqrt 5-1}{2} AB$,根据前面的证明,$CE$ 即为这个正五边形的边长。
以 $CE$ 为半径在作五条弧即可得到正五边形的五个顶点,将正五边形的顶点两两相连后即可得到正五角星,成品:
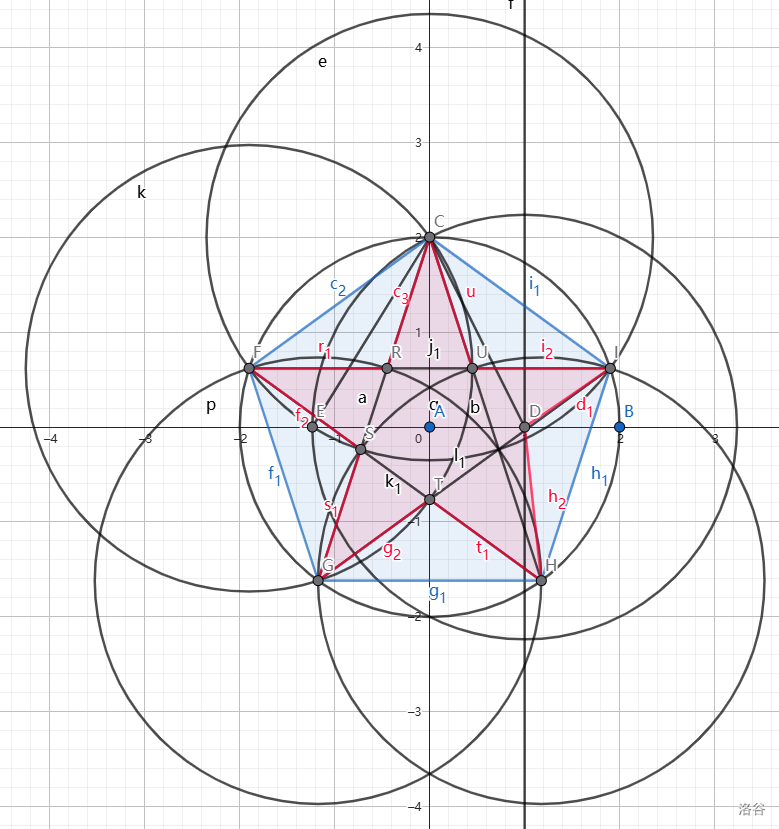
其中蓝色多边形为正五边形,红色多边形为正五角星。
至此,我们成功地尺规出作正五角星。