【普及】最短路专项训练

- **[【旧版】$2019$ 年初版本的最短路讲解](https://www.luogu.com.cn/blog/LinearExpectation/shortest-path-old-version)** - **[【新版】$2021$ 年初版本的最短路讲解](https://www.luogu.com.cn/blog/LinearExpectation/shortest-path-in-another-sight)** 日后会有分层图的内容，当然你也可以直接去搜分层图题单 求收藏qaq ## 前言 Floyd，Bellman-Ford，SPFA，Dijkstra，Johnson，是图论路上绕不去的坑，这一篇博文应该不会介绍 Johnson 最短路算法了，而会重点介绍其余四种的思想内涵。 思想与方法往往比代码的实现更重要，对于一道题目，我们首先认识到他所对应的算法，然后我们应该用自己的大脑来思考（~~而不是用别人的~~）这道题应该按照怎样的逻辑顺序来进行操作——考虑如何通过具体的实现来达到要求的功能，而不是考虑如何修改模板以通过此题——后者往往会是一个痛苦的过程。 该说的话还是要说的，**在阅读本文前，请确保您基本理解 [图论相关概念](https://oi-wiki.org/graph/concept/) 中的大部分内容**，同时也建议您记忆学习一下 **[笔记：四种存图方式](https://www.luogu.com.cn/blog/LinearExpectation/Ways-of-storing-graphs)** 以便理解菜鸡的代码。 参考文献（迫真）： - https://www.luogu.com.cn/blog/ltzlInstallBl/post-suan-fa-bi-ji-dijkstra - https://www.cnblogs.com/bigsai/p/11537975.html - https://visualgo.net/zh/sssp 常见问题： - 为什么要 `#define int long long`？因为 `0x7fffffff` 可能会溢出。 ## Floyd-Warshall：暴力出奇迹 这是一个全源最短路算法。 是的，这意味着我们可以通过他求得所有节点之间的最短路，怎么办呢？事实上，我们可以考虑一个很暴力的办法，接下来我们从输入开始。 我们会读入 $m$ 条边，那么先用邻接矩阵存储起来（由于 Floyd 的时间复杂度是 $O(n^3)$ 的，所以不用担心 $n^2$ 的空间复杂度，并且这里为了存储所有最短路也应该得使用 $O(n^2)$ 的邻接矩阵），接下来，我们将会以 $e_{u,v}$ 表示从 $u$ 到 $v$ 的一条有向边。一开始，他们要么是 $0$，即自己到自己（$e_{x,x}$）；要么是 $\infty$，即没有通路；要么是两点之间的直接道路。 首先对于从 $u$ 到 $v$ 的一条路，如果想要找到最短路，我们肯定要试一试其他的边，也就是“不止经过这两个边直接路径”的路径，那我们假设存在一个桥梁 $k$。 如果 $e_{u,k}+e_{k,v}$ 的长度会小于 $u$ 到 $v$ 的长度，就意味着我们能够更新这个节点了。那么就更新，这样子，我们按顺序更新完所有的节点，就可以获得到一张完整的图——一个被填满的 $e$ 数组，即所有节点之间的最短路。 此时就处理完毕了，注意循环枚举 $k$ 在最外层，内层的 $u$ 和 $v$ 没有顺序要求，一共三层循环，每层循环到 $n$ 为止，所以时间复杂度是 $O(n^3)$ 的。 [【模板】单源最短路径（弱化版）](https://www.luogu.com.cn/problem/P3371) 可以拿到 $70$ 分的 Floyd 程序。 ```cpp #include<bits/stdc++.h> #define int long long #define INF 0x7fffffff using namespace std; int n,m,s; int edge[10005][10005]; void Floyd(){ for(int k=1;k<=n;k++){ for(int i=1;i<=n;i++){ if(i==k||edge[i][k]==INF)continue; for(int j=1;j<=n;j++){ edge[i][j]=min(edge[i][j],edge[i][k]+edge[k][j]); } } } } signed main(){ scanf("%lld%lld%lld",&n,&m,&s); for(int i=1;i<=n;i++) for(int j=1;j<i;j++) edge[i][j]=edge[j][i]=INF; for(int i=1;i<=m;i++){ int u,v,len; scanf("%lld%lld%lld",&u,&v,&len); edge[u][v]=min(edge[u][v],len); }Floyd(); for(int i=1;i<=n;i++){ cout<<edge[s][i]<<' '; }return 0; } ``` 适用的前提是比必须存在最短路，即不能有负环。 ## Bellman-Ford：简单且清晰 我们发现，如果像 Floyd 那样“撒大网捕小鱼”，效率是很低的，所以我们会想要省略一下无用的内容——我们不如更新所有节点的最短路时，就只更新和 $s$ 相关的吧！那我们又该怎么操作呢？ Bellman-Ford 的解决思路是：“所有的最短路都由边组成。”也就是说，如果我们每次松弛 $m$ 条边，就至少能确定一个结点的最短路，这样松弛 $n$ 次之后，我们就能够得到一张完整的“关于 $s$ 的最短路表”了。 因为不知道该用哪一种方法存图（你现在被迫假装不知道），我们就先用邻接矩阵试一试吧（好写，虽然你会发现正解更好写）！ 我们首先需要一个 $k$ 循环 $n$ 次，控制我们松弛的轮数；再来一个二维的循环 $i,j$ 遍历每一条边，每次“如果走了从 $s$ 到 $x$ 的当前最短路+从 $x$ 到 $y$”比“直接走当前 $y$ 的最短路”更快，那最短路就应该要更新了！这被称为一次松弛（$\rm\small relax$）。 代码如下，容易理解： ```cpp #include<bits/stdc++.h> #define INF 0x7fffffff #define MAXN 10005 #define int long long using namespace std; int edge[MAXN][MAXN],dis[MAXN]; int n,m,s; void BellmanFord(){ dis[s]=0; for(int k=1;k<=n;k++){//一共要进行 n 轮松弛 for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ dis[i]=min(dis[i],dis[j]+edge[j][i]); } } } }signed main(){ cin>>n>>m>>s; for(int i=0;i<=n;i++)dis[i]=INF; for(int i=0;i<=n;i++) for(int j=0;j<=n;j++)edge[i][j]=INF; for(int i=0;i<m;i++){ int u,v,w; cin>>u>>v>>w; edge[u][v]=min(edge[u][v],w); }BellmanFord(); for(int i=1;i<=n;i++)cout<<dis[i]<<' '; return 0; } ``` 这时候你发现，这个效率好低啊，怎么看着也是 $O(n^3)$ 啊……不假，确实这种方法效率十分低下，在模板（弱化）中拿到的分数仅 $40$ 分，比 Floyd 还低。为什么？ 原因就在于我们遍历了大量无用的边，试想你要遍历 $n^2$ 条边，而总共只有 $m$ 条边，对于稀疏图（或随机数据）来说，基本满足 $m\ll n^2$，这意味着我们应该用一种能够遍历所有边而不浪费时间的方式。 什么方式呢？邻接表？链式前向星？ 错，直接存边。 这样我们就能遍历这 $m$ 条边，而这样的方法复杂度是 $O(mn)$，也就是 $n$ 轮松弛每次 $m$ 条边。这样的方法（大常数）能在弱化版获得 $70$ 分，和 Floyd 一样（比 Floyd 期望分数高）。 代码： ```cpp #include<bits/stdc++.h> #define INF 0x7fffffff #define MAXN 10005 #define int long long using namespace std; struct edge{ int u,v,w; }e[500005]; int edge[MAXN][MAXN],dis[MAXN]; int n,m,s; void BellmanFord(){ dis[s]=0; for(int k=1;k<=n;k++){//一共要进行 n 轮松弛 for(int i=1;i<=m;i++){ int u=e[i].u,v=e[i].v,w=e[i].w; dis[v]=min(dis[v],dis[u]+w); } } }signed main(){ scanf("%lld%lld%lld",&n,&m,&s); for(int i=0;i<=n;i++)dis[i]=INF; for(int i=1;i<=m;i++){ int u,v,w; scanf("%lld%lld%lld",&u,&v,&w); e[i].u=u;e[i].v=v;e[i].w=w; }BellmanFord(); for(int i=1;i<=n;i++)cout<<dis[i]<<' '; return 0; } ``` 但是这样凌乱地松弛（跳来跳去），总感觉有些混乱和浪费啊，难道我们不能做到“有目的”地松弛吗？我们为什么要去松弛那些“相关节点”都没有被更新过的边啊，这也不能得到任何新的结果啊？ 诶，对了，这启发了我们。 ## SPFA：虽死犹光荣 **算法概括**：每一次松弛之后，只有与松弛结点 $x$ 相邻的节点（的最短路长度）才可能会被更新，于是我们可以开始松弛这个节点。那么，我们改如何安排我们松弛的顺序呢？ 用队列——是的，SPFA 是 Bellman-Ford 的队列优化，通过队列保证我们每次进行松弛都有结果，这样我们就能获得一个（上界复杂度不变的）优化算法。我们的操作是这样的：每次松弛一个节点，就将他的相邻节点入队，然后取出队头进行操作。 接下来我们详细地进行讲解： Bellman-Ford 中有相当一部分操作事实上是无用的，核心思想是在每一轮松弛中更新**所有节点**到起点，而这带来了一个问题，对于正在计算的节点 $u$，如果紧接着计算他的相邻节点，那么一定会有一个结果——无论是否更新，都完成了一次**有效的松弛**。这种操作可以加速收敛的过程，而进一步思考：有哪些节点需要入队？ 我们应该把最短路状态有变化的节点入队，因为只有他们才会影响我们下一步的更新。而此时出现了一个问题——一个入过队的节点 $u$，可能在之后的松弛中再次更新，这一点直接影响了这一算法的效率：反复入队的节点可能很少也可能很多，这取决于图的特征，并且： > 即使两个图的节点和边数完全一样，仅仅是几条边的权值不同，他们的 SPFA 队列也会差距很大，如此感性上理解，**SPFA 是不稳定的**。 这里给出 SPFA 的代码： ```cpp #include<bits/stdc++.h> #define int long long using namespace std; const int MAXN=1000005; struct edge{ int to,nxt,w; }e[MAXN]; int n,m,cnt,s,head[MAXN]; int dis[MAXN]; bool inq[MAXN];//inq[i]=1 表示 i 在队列里 void init(){ for(int i=0;i<MAXN;i++){ e[i].nxt=-1; head[i]=-1; inq[i]=0; dis[i]=0x7fffffff; }//初始化链式前向星和入队标志 }void addedge(int u,int v,int w){ e[cnt].to=v; e[cnt].w=w; e[cnt].nxt=head[u]; head[u]=cnt++; }void SPFA(){ dis[s]=0;queue<int>q; q.push(s);inq[s]=1; while(!q.empty()){ int u=q.front();q.pop(); inq[u]=0; for(int i=head[u];~i;i=e[i].nxt){ int v=e[i].to,w=e[i].w; if(dis[u]+w<dis[v]){//如果可以更短 dis[v]=dis[u]+w;//松弛 if(!inq[v]){//如果不在队里 inq[v]=1;//就入队 q.push(v); } } } } }signed main(){ scanf("%lld%lld%lld",&n,&m,&s); init();//初始化 for(int i=0;i<m;i++){ int u,v,w; scanf("%lld%lld%lld",&u,&v,&w); addedge(u,v,w); }SPFA(); for(int i=1;i<=n;i++)printf("%lld ",dis[i]); return 0; } ``` 这个程序能通过弱化数据版本，强化数据版本为 $32$ 分，改成优先队列时 $52$ 分，改成栈是 $68$ 分，但是栈版本不能通过弱化数据。建议大家不要乱改，有时会有严重的后果。 先给大家看一段话： > 众所周知 SPFA 可以看做是 Bellman-Ford 的队列优化。 Bellman-Ford 每轮松弛会使最短路的边数至少 $+1$，而最短路的边数最多为 $n−1$，则其复杂度上界是稳定的 $O(nm)$ 的。 > > ——[「笔记」如何卡 Spfa](https://www.cnblogs.com/luckyblock/p/14317096.html) 但是 SPFA 能被卡，能被卡到 Bellman-Ford 的复杂度，我们先讲原因，再讲方法： > 究其原因，要从 SPFA 是 Bellman-ford 的优化说起。在 $n$ 个点 $m$ 条边的图中，Bellman-ford 的复杂度是 $n\times m$，依次对每条边进行松弛操作，重复这个操作 $n-1$ 次后则一定得到最短路，如果还能继续松弛，则有负环。这是因为最长的没有环路的路，也只不过是 $n$ 个点 $n-1$ 条边构成的，所以松弛 $n-1$ 次一定能得到最短路。 > > SPFA 的意义在于，如果一个点上次没有被松弛过，那么下次就不会从这个点开始松弛。每次把被松弛过的点加入到队列中，就可以忽略掉没有被松弛过的点。 > > 但是最外层的循环还是 $n-1$ 次。如果把被松弛的点放到前边，他相当于没有进行完这一轮松弛，就开始了一些其他的操作。但是这些其他的操作可能是无用的，因为这些操作的起始点可能还会被这一轮松弛更新。 > > 所以传统的 SPFA 的复杂度不会超过 $n\times m$，并且每个点都不会第 $n$ 次入队。 渐进意义上，他的复杂度依然是 $O(nm)$，一共只有 $m$ 条边所以每个节点最多只会入队 $m$ 次。SPFA 在本质上只是改变的入队的顺序，其复杂度上界依然是 $O(nm)$，接下来介绍卡法（[参考资料](https://www.zhihu.com/question/292283275)）： **普通 SPFA**： 链套菊花，可以让这个菊花节点反复被入队，造成时间的大量浪费。或者我们可以构造一个具有大量次短路的网格图，使得 SPFA 容易一错到底，即“在网格图中走错一次路可能导致很高的额外开销”。我们可以考虑构造一个网格图套菊花，或者把两种方法结合起来，放在同一个 Subtask 中。 **LLL 优化**： 方法是比较入队的边权与 $ave$（平均值），如果更大则插入到队尾。卡死的方法是向 $1$ 连接一条权值极大的边。 **NTR 优化**： https://www.zhihu.com/question/268382638/answer/337778164 没看懂，将就着看看吧。 **SLF 优化**： 极其广为人知的优化，每次将入队结点距离和队首比较，如果更大则插入至队尾。依然可以用链套菊花的方式卡，“链上用几个并列在一起的小边权”。带容错的版本依然可以通过高边权和的方式卡死。 如果是 $\rm swap$ 版本的“每当队列改变时，如果队首距离大于队尾，则交换首尾。” 也可以用类似的方法卡死。 那么，我们怎么样能够把它卡到 $2^n$ 级别呢（有负权的情况）？这就可以参考 [\[HDOJ 4889\] Scary Path Finding Algorithm \[SPFA\]](https://blog.csdn.net/jinzhao1994/article/details/38311561?depth_1-) 的方案，可以发现，SLF 其实不是一个优化，反而在某些情况下会起到极其恐怖的负优化效果，“它丢掉了一轮一轮松弛的这个特性，导致复杂度可能呈指数级上升”。 这里给出一个结论（建议）： - Dijkstra 是正权图上数学严格证明的最优算法，优先学习。 - 写 SPFA 的时候当做 Bellman-Ford，其**复杂度并非更优**而是随机图跑得快而已。 为什么我们说 Dij 稳定？因为他带有标记，每个节点的计算次数是有限度的，并且从 $O(n^2)$ 优化到 $O((m+n)\log n)$ 是不难的。 ## Dijkstra：正统最短路 ### Dijkstra 基础 现在我们很有钱，一共有 $n$ 个节点，$m$ 条边（大概是有向边），以及一个初始节点 $s$，要求我们求出从 $s$ 到其他所有节点的最短路，怎么办呢？ 首先我们需要一个数组 $d$，用于存储从 $s$ 到 $1\sim n$ 的最短路长度，表示为 $d_1\sim d_n$。于此类似的，我们需要一个 $e$ 数组来存储整张图，$e_{u,v}$ 表示从 $u$ 到 $v$ 的路径长度。此外，我们还需要一个数组 $vis$ 来确定从 $s$ 到一个节点的最短路是否被确定了。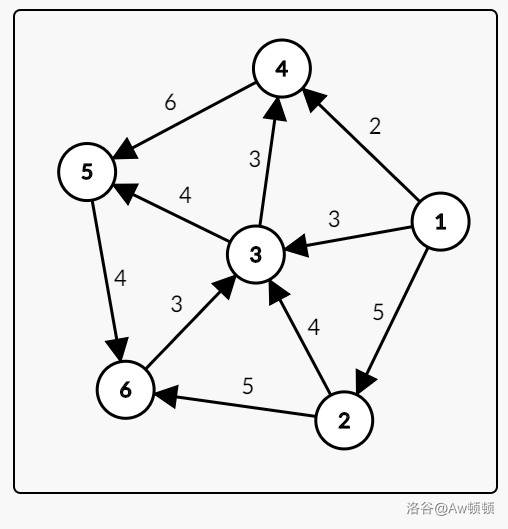 首先，我们可以把 $s$ 的所有出边都加入到 $d$ 数组中，譬如这个图：  如果令 $s=1$，那么它的 $d=\{0,5,3,2,\infty,\infty\}$ 接着我们需要在这个数组中找到最小的那个节点——也就是离出发点最近的那个节点，你会发现，这个记得点是 $4$，那么我们考虑走向 $4$ 号节点。 这时这个 $4$ 号节点的最短路就已经确定了，为什么？因为如果走任何一条其他路，刚走第一步就会比这条最短路要长，所以，直接走到 $4$ 必然比绕其他的路要来的短。那么，我们标记 $4$ 为已经确定最短路的点 接着我们要做的是考察 $4$ 号节点的所有出边，这时你需要看一看的是，如果我们从 $4$ 经过再到某个节点 $x$，会不会比直接从 $1$ 到 $x$ 更近？如果是的，那么更新最短路就可以了。 你发现 $1\to 4\to 5$ 长度为 $8$，比 $d_5=\infty$ 要小多了，那么更新吧！此时的的 $d=\{0,5,3,2,8,\infty\}$ 这时，未确定最短路的点中，最小的是 $3$ 了，那就走向 $3$ 吧，并且把他标记为已经确定。$3$ 的出边指向 $4,5$，此时执行如下： - $(1\to 3\to 4)>(1\to 4)$，不需要更新。 - $(1\to 3\to 5)<(1\to 4\to 5)$，需要更新。 这时候发现有一条路比原有的 $d_5$ 更小！那么就可以更新了更新完是这样：$d=\{0,5,3,2,7,\infty\}$。此时的 $vis$ 数组中 $1,3,4$ 都已经被确定了。我们把目光投向 $2$。 继续更新！此时的 $2$ 一共有 $3,6$ 两个出边，作类似的判断之后我们发现只有 $6$ 可以更新，那么 $d=\{0,5,3,2,7,10\}$，$vis={1,2,3,4}$。 接着的更新内容就简单地概述了： - 看向 $5$ 号节点。 - 更新不了节点，$5$ 号设为确定。 - 看向 $6$ 号节点。 - 更新不了节点。 算法结束。这时候你会发现，有一部分边是没有走过的，我们只遍历了一些点，并且一直在走“权值最小”的那条路。这似乎是贪心，那么，他为什么正确呢？ 对于一个不含负边的图，全局最小值不可能再被其他节点更新，因为每当 $x$ 被纳入了 $vis$ 数组，他的最短路就已经确定了，正如前文所说：“如果走任何一条其他路（走已经更新的最短路），所使用长度必然的比当前这条最短路要长，所以，现在这条老路不可能再被其他已确定最短路更长的路径更新了。” 由于这种算法不包含后悔的情况，所以不能应对含负权边的图。 由于有 $n$ 个节点，每个节点必然走过一次，且每次都需要在 $n$ 个 $d_i$ 中找最小值，且每次都要在找所有的出边，所以时间复杂度是 $O(n^2)$ 的。 ### Dijkstra 优化 我们发现，在 $d$ 数组中找到最小值的这个过程可以优化，怎么优化呢？ 如果用堆优化是 $O(m\log n)$，如果用优先队列时 $O(m\log m)$。但是也有说法说堆优化是 $O((n+m)\log n)$，似乎还挺优秀的。 由于 $m$ 最大时可以达到 $n^2$ 级别，所以时间复杂度看着办吧。似乎对于普通的数据并不容易出现 $m=n^2$ 这种情况（稠密图），所以对于随机数据，你可能可以选择卡常而不优化，但是面对刻意为之的数据，你不得不承认：这个优化是广泛而且有效的。 接下来的代码用链式前向星存图，如果不会请回到本文开头找资料。 首先你需要一个 $\rm\small node$ 类型，这种类型包含两个信息：$\rm\small id,dis$，分别是上文所说的“下标”和“距离起点的长度”。下标也就是这个节点的编号。接着我们重载运算符，让 $<$ 比较的“依据”是距离起点的长度，这样我们导入优先队列时，就自然按照距离排序，我们也就能够很容易取出“距离最短”的那个点了。 这一段的参考代码： ```cpp struct node{ int dis,id; bool operator <(const node &x)const{ return x.dis<dis; }//重载运算符，比较节点的方式是比较其相距起点的距离 //便于之后使用优先队列比较 }; ``` 然后我们每次取出队头、弹出就行了。注意一些小优化： - 处理 $x$ 节点时，如果他已经被处理过，就跳过。 为什么“已经确定”的节点还会再遇到一次？这是因为优先队列只能对队头进行操作，不能够实现删除任意元素，所以我们每次松弛都要压入。那这样为什么不会影响正确性呢？因为我们每次取出节点，都是取它“所有在队列中值”最小的那个，而既然“最小”，必定更符合要求，所以是正确的的。 - 遍历 $x$ 的出边 $y$ 的时候，如果处理过，就跳过。 没什么有用的优化，但是看着代码逻辑更清晰。 这里给出全文代码，可以结合注释理解。 ```cpp #include<bits/stdc++.h> using namespace std; #define int long long #define MAXN 1000005 #define MAXM 2000005 #define INF 0x7fffffff struct edge{ int to,w,nxt; }e[MAXM]; int head[MAXN],dis[MAXN]; int n,m,s,cnt; bool sure[MAXN];//通往该节点的最短路是否确定 struct node{ int dis,id; bool operator <(const node &x)const{ return x.dis<dis; }//重载运算符，比较节点的方式是比较其相距起点的距离 //便于之后使用优先队列比较 }; void addedge(int u,int v,int w){ e[cnt].w=w;//权值为 w e[cnt].to=v;//终点为 v e[cnt].nxt=head[u];//接到 u 的 "邻居链表" 开头 head[u]=cnt++;//把 "开头 " 更新为这条边 }void init(){//初始化 for(int i=0;i<=n;i++){ head[i]=-1;//尚未连边 e[i].nxt=-1;//每个节点都没连边 }cnt=0;//一条边都没有 }priority_queue<node>q; void Dijkstra(){ dis[s]=0;q.push((node){0,s});//压入起点 while(!q.empty()){ node cur=q.top();q.pop();//当前处理的节点 int x=cur.id,d=cur.dis; if(sure[x])continue;//如果这个节点的最短路已经确定，跳过 sure[x]=1;//否则标记为确定，并且开始着手确定 for(int i=head[x];~i;i=e[i].nxt){//遍历出边 int y=e[i].to;//取出这条边 if(sure[y])continue;//如果取出了，就跳过 if(dis[y]>dis[x]+e[i].w){//如果路径更短 dis[y]=dis[x]+e[i].w;//松弛 q.push((node){dis[y],y});//加入队列 } } } }signed main(){ scanf("%lld%lld%lld",&n,&m,&s); init();//初始化 for(int i=0;i<=n;i++)dis[i]=INF;//全部设为 INF for(int i=0;i<m;i++){ int u,v,w; scanf("%lld%lld%lld",&u,&v,&w); addedge(u,v,w); }Dijkstra(); for(int i=1;i<=n;i++)printf("%lld ",dis[i]); return 0; } ``` 之所以能应对重边，因为你存储的时候会把两个边都存下来。